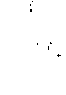Vector Model of Angular Momentum

[Rapier]

Homework Statement

The vector model of angular momentum is a mnemonic device which illustrates the quantization of angular momentum and the restriction that only one of component can be specified. By convention that component is taken to be in the z direction. The figure below represents an example of the vector model. The radius of the circle has a length of 3.653 x 10-34 J-s.


a) What is the orbital angular momentum quantum number, l, represented by this figure?.
l = 3. *
OK

As shown in the figure the angle between the z-axis and the angular momentum vector, θ, is 106.779°.

b) What magnetic orbital angular momentum quantum number, ml, does this orientation represent?

ml = -1. *
OK

c) What is the projection of the angular momentum vector, Lz, along the z-axis in units of J-s?,

Lz = J-s.
-2.872276 NO

Other allowed values of the magnetic orbital angular momentum quantum number would be represented in the diagram by other vectors.

d) Following the rules of the vector model, what is the total number of vectors that could be drawn in the figure.

The total number of allowed vectors is 7. *
OK

Suppose that we are considering the angular momentum of an electron. An electron with orbital angular momentum, L, has an orbital magnetic moment, μ. The two vectors are related by \mu= (-e/2m)*L.

Recall from Electricity and Magnetism that the potential energy of a magnetic dipole in a magnetic field is U = -\mu*B.

Suppose that a magnetic field of B = 0.9 Tesla is applied in the z direction.
e) What is magnetic potential energy in eV of the electron in the state represented by the figure? (Note the sign.)

U = eV.

f) What is the difference in energy in this magnetic field between states of this orbital angular momentum which differ in their orbital magnetic quantum number by one? (The answer is a positive number.)

DU = eV.

A magnetic moment in a magnetic field experiences a torque (Physics 112 Lecture 13, click here.) The torque causes L to precess about the z-axis, the component of L along the z-axis, Lz, remaining unchanged.

g) Does the rotational kinetic energy and magnetic potential energy of the electron change because of this motion? Answer 1 for does, or 2 for does not.

The energy of the electron change due to its motion in the magnetic field. *
2 OK

Homework Equations

The Attempt at a Solution

I am having problems calculating L in part C, which I will need in parts E and F. I have tried a couple of different equations and I am not getting the right answer. I would have included a relevant equation and some of my work but it covers nearly two full pages of wrong answers. I am terribly stuck!

Thanks for all the help.

 

[Rapier]

I was making Part C harder than necessary.

Lz = -1.05455e-34 Js

But now I am stuck again on parts E and F. I am having problems calculating the potential energy based upon my information.