bvschaefer
- 1
- 0
Homework Statement
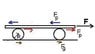
A plank with a mass M = 6.30 kg rides on top of two identical, solid, cylindrical rollers that have R = 5.30 cm and m = 2.00 kg. The plank is pulled by a constant horizontal force Farrowbold of magnitude 5.00 N applied to the end of the plank and perpendicular to the axes of the cylinders (which are parallel). The cylinders roll without slipping on a flat surface. There is also no slipping between the cylinders and the plank.
(a) Find the initial acceleration of the plank when the rollers are equidistant from edge of the plank
(b)Find the acceleration of the rollers at this moment
(c)What friction forces are acting at this moment? (Fg and Fp)
Homework Equations
F = ma
T = Iα
T = F x R
The Attempt at a Solution
Using parallel axis theorem, I have:
I = Icm + MR2
I = .5(2.00kg)(.053)2 + (2.00kg)(.053)2
I = 0.00841
where point of rotation is at the ground.
From here, I know I have to use a torque equation to solve for acceleration but am stuck, any help is appreciated!