toothpaste666
- 516
- 20
Homework Statement
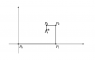
Let \{P_i\}_{i=0}^\infty be a sequence of points on a plane. Suppose P_is are placed as on the picture below, so that |P_0 P_1|=2, |P_1 P_2|=1, |P_2 P_3|=.5, |P_3P_4|=.25, ... Find the coordinate of the point P = \lim_{i→\infty} P_i
Homework Equations
The Attempt at a Solution
here are the points P_0: (0,0) P_1: (2,0) P_2: (2, 1) P_3: (1.5, 1) P_4: (1.5, .75) P_5: (1.625, .75)
lets examine the x values first:
2, 1.5, 1.625
this is a sequence defined recursively by:
a_1 = 2
a_{n+1} = 2 - \frac{a_n}{4}
L = \lim_{a_n\rightarrow\infty} a_n = \lim_{a_n\rightarrow\infty} a_{n+1} <br /> = \lim_{an\rightarrow\infty} 2-\frac{a_n}{4}
which means that
L = 2-\frac{L}{4}
4L = 8 - L
5L = 8
L = \frac{8}{5}
L = 1.6
so 1.6 would be the x coordinate of the point.
I then would follow a similar process to find the y coordinate, but before I do that I just want to make sure what I have so far is correct.