Classical mechanics Definition and 1000 Threads

Firstly, There is something I want to clarify. When the system starts moving, parts of the chain that still lies on the table, which have mass ## \frac {(L- y_0)M} {L}##, will be pulled by the force that the hanging chain's weight exert,right? If yes, then : As far as I know, the formula ##F=...

Hi all, Consider a system of ##N## noninteracting, identical electric point dipoles (dipole moment ##\vec{\mu}##) subjected to an external field ##\vec{E}=E\hat{z}##. The Lagrangian for this system is...

I don't attempt solving a problem until I fully understand it, conceptually. After the hit (when maximum velocity is reached) the person starts losing momentum, having a constant upwards acceleration. The forces acting on the person are gravity and the normal to the ground. $$N - mg = ma$$...

Books that teaches classical mechanics through a discourse method ie asking interesting questions and answering them maybe a similar one to Understanding Basic Chemistry Through Problem Solving: The Learner's Approach Book by Jeanne Tan and Kim Seng Chan. Not exactly asking numerical questions...

(a) ##u_{min}=\big(1+\frac{m_2}{m_1}\big)\sqrt{2\mu_k g d}## (b) ##x_f=\sqrt{\frac{2h}{g}\Big(\big(\frac{m_1}{m_1+m_2}u\big)^2-2\mu_k g d\Big)}## Can someone check please?

Someone pls solve this. I've done it but I'm not sure if it's correct. Thanks!

Hello, I have posted a similar thread on this question before, but I'd like to get some help to simplify the answers I've got so far in order to match the solutions provided. If anyone could help me, I would really appreciate it. Since (c) is quite similar to (b), I'll leave here what I've done...

Hello, I'm having some trouble understanding this solution provided in Landau's book on mechanics. I'd like to understand how they arrived at the infinitesimal displacement for the particles m1. I appreciate any kind of help regarding this problem, thank you!

So I've been studying classical mechanics and have come across a small doubt with the solution provided to the problem in question from Landau's book. My question is: why are the coordinates for the particle given as they are in the solution? I imagine it has something to do with the harmonic...

Image above is the question. Below image depicts solution. if F1 is removed then the acceleration of that mass must be sum of accelerations of remaining forces. Right?? But answer says that acceleration of that mass is equal to acceleration of F1. I don't understand it. Can someone explain it??

I used the Change in Kinetic Energy and equated that with the Work Done. The "Work Done" part comprises of two different functions- one is work done by Gravitational Force while the other is the work done by frictional force (or the brakes). /Delta KE (magnitude wise)= 0.5*1350* (20^2)=270,000...

$$x(t)=\int \dot{x}(t)\mathrm dt=vt+c$$ That's what I did. But, book says $$x(t)=\int \dot{x}(t)\mathrm dt=x_0+v_0 t+ \frac{F_0}{2m}t^2$$ Seems like, $$x_0 + \dfrac{a_0}{2}t^2$$ is constant. How to find constant is equal to what?

> >A stuntman jumped from $1.25 \ \text{m}$ height and, landed at distance $10 \ \text{m}$. Find velocity when he jumped. (Take $\text{g}=10 \ ms^{-2}$) I had solved it following way. $$h=\frac{1}{2}gt^2$$ $$=>1.25=5\cdot t^2$$ $$=>t=\frac{1}{2}$$ And, $$s=vt$$ $$v=\frac{s}{t}$$ $$=\frac{10 \...

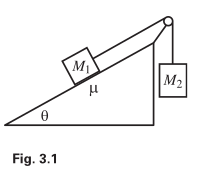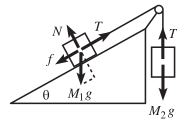><br/> >Mass M1 is held on a plane with inclination angle θ, and mass M2 hangs over the side. The two masses are connected by a massless string...

>Mass of a timber is $20 \ g$. And, density of that timber is $0.27 \ g/cc$. That timber was bind to a metallic materials and, it was released to $0.970 \ g/cc$ water. How much the wood was submerged in water? I was trying to solve the problem following way. $$F=Ah\rho g$$ $$=V\rho g$$ $$=V \...

I have read Classical Mechanics book by David Morin, and there are some parts that I do not understand from its derivation. Note : ## V## and ##v## is respectively the velocity of CM and a particle of the body relative to the fixed origin , while ##v'## is velocity of the particle relative to...

So far all I have determined is the equations of motion for the two and that is as follows. It is trivial that y(t)=v1sin(Q)t -gt^2/2 and that x(t)=v2cos(Q)t. Now the angle that is anticlockwise from the negative horizontal of the robber is 90 - Q using basic trigonometry, using this we can...

1.One can now see why all bodies fall at same rate: A body of twice the weight will have twice the force of gravity pulling it down, but it will also have twice the mass. According to Newton’s second law these two effects will exactly cancel each other, so the acceleration will be same in all...

I'm trying to solve the Goldstein classical mechanics exercises 1.7. The problem is to prove: $$\frac{\partial \dot T}{\partial \dot q} - 2\frac{\partial T}{\partial q} = Q$$ Below is my progress, and I got stuck at one of the step. Now since we have langrange equation: $$\frac{d}{dt}...

I am trying to find the equations of motion of the angular momentum ##\boldsymbol L## for a system consisting of a particle of mass ##m## and magnetic moment ##\boldsymbol{\mu} \equiv \gamma \boldsymbol{L}## in a magnetic field ##\boldsymbol B##. The Hamiltonian of the system is therefore...

I have attached two different attempts to solve this problem. They both look correct to me but they give two different answers! Which one is correct, which one is wrong and why?

In Classical Mechanics by Kibble and Berkshire, in chapter 12.4 which focuses on symmetries and conservation laws (starting on page 291 here), the authors introduce the concept of a generator function G, where the transformation generated by G is given by (equation 12.29 on page 292 in the text)...

Hi! I am an engineering graduate that took my bachelor's degree in Mechanical Engineering much too long ago, but I have forgotten a lot of the classical mechanics/mechanics of materials theory that I had learned many years ago. I am building a motorcycle right now, and I want to calculate the...

What we know: The ball is dropped at the tip A with some speed ##v_0## and rebounds with speed ##v##. This collision produces an angular impulse, changing the angular momentum of the bar with the flywheels. Solution inspired by an answer provided by @TSny in the similar question. Angular...

Hi. So I was asked the following question whose picture is attached below along with my attempt at the solution. Now my doubt is, since the question refers to the whole system comprising of these thin rigid body 'mini systems', should the Principle moments of Inertia about the respective axes...

I've already found the potential and force that produce the given orbit. my results were: ##V=-\frac{al^2}{mr^3}## ##\vec{F}=-\frac{-3al^2}{mr^4}\hat{r}## Now, I've been trying to find the period using the equation ##t=\sqrt{\frac{m}{2}}\int_{r_0}^{r}\frac{dr'}{\sqrt{E-V_{eff}}}## Using...

I solved this problem easily using Newton's second law, but I had problems trying to use mechanical energy conservation to solve it. How I solved using Newton's second law: ##\text{(part of the rope that is on the left)}\, m_1=x\rho g,\, \text{(part of the rope that is on the right)}\...

I understand that when $$A_0 \gg g$$, the g term in the equation of motion can be dropped. The equation of motion then becomes $$\frac{d^2\theta}{dt^2}=-\frac{a_d(t)}{L}\sin\theta$$ But how can I show that the pendulum is stable for such case? I am totally clueless.

My doubt is with Method 2 of the given example in KK. I'm unable to understand why the torque around A (where we have chosen a coordinate system at A) becomes zero due to the R x F in z direction with a minus sign {Photo Attached} I have tried to reason out that one way to formulate that term...

We were prescribed Goldstein, Taylor and Marion/Thornton for our first course in analytical mechanics, and I'm about to finish up the course but I feel like I have not gotten a good physical, intuitive grasps of the concepts, so I've been trying to read the texts a bit more. Taylor and...

I think it could be interesting. Consider a mechanical system A circle of mass M can rotate about the vertical axis. The angle of rotation is coordinated by the angle ##\psi##. A bead of mass m>0 can slide along this circle. The position of the bead relative the circle is given by the angle...

I have several* classical physics and mechanics texts, and none solve the Kepler problem (as far as I can tell), succinctly, solving the Kepler equation, M = E - e*sin(E), for E given M and e, or more generally determining the equations of motion for an orbiting object. In fact none even...

I tried 1. using the Lagrangian method: From ##y=-kx^2## I got ##\dot y = -2kx \dot x## and ##\ddot y = -2k \dot x^2 - 2 kx \dot x##. (Can I use ##\dot y = g## here due to gravity?) This gives for kinetic energy: $$T = \frac{1}{2} mv^2 = \frac{1}{2} m (\dot x^2 + \dot y^2) = \frac{1}{2} m (\dot...

Why is the action a scalar? Please explain.

Hello to everyone :smile: I'd like to study this problem. You have a 2D guide, described by an equation y = y (x) in a reference interval x ∈ I = [a, b], placed in a cartesian vertical plane Oxy. The guide is frictionless and the only force that is acting is the gravity force. On this track, a...

Hi! i need some textbooks recommendations to learn by my self about classical mechanics in a undegraduate level. I don´¨¨t know what kind of math is required, i have knowledge about calculus by my high school classes and i learned more with the book "Calculus" by Gilbert Strang. I wait for your...

In high school I learned about three kinds of motion in classical mechanics - translation, rotation, and oscillation. Are there any other kinds of motion in the physical world?

If you take a rubber band and fix it in a stretched position for an extended period of time, would it eventually lose its elasticity? If yes, then how can you calculate how long it would take until its elasticity decreases by a certain amount, say, fifty percent? If no, why not? How does the...

In special relativity (especially relativistic collisions), is the center of mass frame as useful as Newtonian mechanics?

The hamiltonian ´for a free falling body is $$H = \dfrac{p^2}{2m} + mgy$$ and since we are using cartesian coordinates that do not depend on time and the potential only depends on the position, we know that ##H=E##. For this hamiltonian, using the Hamilton's equations and initial conditions...

I've finished with Gregory's classical mechanics and was looking for something a bit more challenging. I thought Arnold's methods of classical mechanics look pretty interesting, but it's definitely more mathematically complex than anything I would have done before, especially the bits about...

Hello, using computation simulation, can the statistical behavior of many particles be derived through deterministic classical mechanics?

Hello forum, i want to make a samulation of a body. The body will be moved horisontal on y,x axis. I want on my simulation the body to change direction many times(for example i want to go for 10sec right and then left end right...). My question is does i need more than one differential equation...

What came to my mind for this question is: Consider one of the cars. The velocity and mass of this car are V and M respectively. And the velocity and mass of the piece attached to the car are m, v respectively. Before the collision, the velocity of this piece relative to this car is zero. So its...

Attempt: By drawing the Free Body diagrams and calculating the different tensions, I got the following results ##T_1=\frac{(M_1+M_2)}{2}g## ##T_2=\frac{\sqrt 3(M_1+M_2)}{2}g## ##T_3=M_2g## But, I am not sure what the answer is as although ##T_2>T_1## but ##T_3## does not depend on ##M_1##...

problem in this book : classical mechanics goldstein Why can we cancel the derivative of dt from these equations? e.g. ##\frac{d(x)}{dt} + \frac{b sin\theta}{2} \frac{d(\theta)}{dt} = asin\theta \frac{d(\phi)}{dt}## ## x +\frac{b \theta sin\theta}{2} = a \phi sin\theta ## because I think...

Let's say I place a positive point charge inside a hollow conducting sphere. If we take a Gaussian surface through the material of the conductor, we know the field inside the material of the conductor is 0, which implies that there is a -ve charge on the inner wall to make the net enclosed...

if the tiny block moves downward by an amount x, the wedge should also move forward by the same amount x as they are connected by the same string whose length has to remain constant, (by differentiating it wrt time we get speed) hence I concluded that v1 = v2, but my book says otherwise what is...