Distribution Definition and 1000 Threads
-
T
Graduate Is Quantum Mechanics Bound by the Limits of Pure Chance?
I recently had a discussion with someone about Quantum Mechanics. His story was confusing to me but I could detect that he made an error in his thinking which I proceeded to explain : You are trying to reason from the idea that the 'collapse of the wave-function', which precedes the...- The Adversary
- Thread
- Distribution Function Probability Pure
- Replies: 27
- Forum: Quantum Physics
-

Charge distribution on the surfaces of parallel conducting s
Problem: Consider two parallel and large sheets with a surface area . One has a charge and the other is uncharged. q | | | | | | | | | | What would be the electric fields on the three regions as divided by the sheets ? General solution to problems like as told...- amind
- Thread
- Charge Charge distribution Conducting Distribution Electrostatics Parallel Surfaces
- Replies: 4
- Forum: Introductory Physics Homework Help
-
W
Conditional Expectation of Multiple Independent Random Varia
Homework Statement Given X,Y,Z are 3 N(1,1) random variables, (1) Find E[ XY | Y + Z = 1] Homework EquationsThe Attempt at a Solution I'm honestly completely lost in statistics... I didn't quite grasp the intuitive aspect of expectation because my professor lives in the numbers side and...- whitejac
- Thread
- Conditional Conditional expectation Distribution Expectation Gauss Independent Integration Multiple Pdf Random Statistics
- Replies: 7
- Forum: Calculus and Beyond Homework Help
-
K
Graduate Boltzmann distribution derivation.
please check the video at 5:33. how can we find the partial derivative w.r.t n1 n2 and on? isn't each state (n1, n2 and on) one discrete state not a continuous variable? is it because we can have multiple particles in the given energy state? However its a finite discrete number. as far as I...- kidsasd987
- Thread
- Boltzmann Boltzmann distribution Derivation Distribution
- Replies: 1
- Forum: Thermodynamics
-
A
Entropy of the distribution as a function of time
I am having an issue with finding the entropy in my program. I was asked to the find the entropy of the distribution as a function of time but i do not know where to start with entropy. I understand entropy but putting it in my program is where I am stuck Here is my code: # -*- coding: utf-8...- alex steve
- Thread
- Distribution Entropy Function Time
- Replies: 2
- Forum: Programming and Computer Science
-
J
Undergrad Understand the T Distribution: What You Need to Know
So my understanding of the T distribution is that if you do not know the variance of a population you estimate the distribution of the mean with the T distribution. But I am not sure about this because if you know the variance of the population, law of large numbers shrinks the variance...- Josh S Thompson
- Thread
- Distribution
- Replies: 19
- Forum: Set Theory, Logic, Probability, Statistics
-
J
Undergrad Normal distribution and constant variance
Why do people say that RVs that have the normal distribution has a constant variance. What does that mean constant variance.- Josh S Thompson
- Thread
- Constant Distribution Normal Normal distribution Variance
- Replies: 3
- Forum: Set Theory, Logic, Probability, Statistics
-
N
Temperature distribution with heat generation
hey i really need help with solving this question. 1. Homework Statement the problem is in one dimension x ( 2 plates with diffrent K joined together) for x=0 T=500 ( constat temp) 0<x<L - electric wire is generating heat that maintane the constant temp in x=0 ,it has K=40W/mK. L<x<2L - there...- noName2
- Thread
- Distribution Generation Heat Temperature
- Replies: 9
- Forum: Engineering and Comp Sci Homework Help
-
Q
Graduate Continous limit of a multivariate normal distribution
Hello everyone, I am currently considering a set of random variables, \vec{x} = [x_1,x_2,...x_N] which are know to follow a multivariate normal distribution, P(\vec{x}) \propto \mathrm{exp}(-\frac{1}{2}(\vec{x}-\vec{\mu})^\mathrm{T}\Sigma^{-1}(\vec{x}-\vec{\mu})) The covariance matrix Σ and...- QuantizedFun
- Thread
- Distribution Fisher information Limit Multivariate Normal Normal distribution
- Replies: 6
- Forum: Set Theory, Logic, Probability, Statistics
-
J
Graduate Same Moment Generating Function, Same Prob. Distribution
How do you know that if two random variables have the same moment generating function then they have the same probability distribution.- Josh S Thompson
- Thread
- Distribution Function Moment
- Replies: 1
- Forum: Set Theory, Logic, Probability, Statistics
-
S
How Do Poisson and Binomial Distributions Apply to Wire Flaw Analysis?
Homework Statement We assume that the number of structural flaws on a long wire have obey Poisson distribution law. On average we find 1 flaw every 5 meters. a) What is the probability that a 20 m long section will have maximum 2 flaws? b) We slice the wire into 1 m long sections. What is the...- skrat
- Thread
- Distribution Poisson Poisson distribution
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-
K
Graduate Derivation of Fermi-Dirac distribution
http://ecee.colorado.edu/~bart/book/book/chapter2/pdf/ch2_5_5.pdfcan you please tell me where f/(f(gi,fi) is from? and also how to get to (2.5.13)- kidsasd987
- Thread
- Derivation Distribution Fermi-dirac Fermi-dirac distribution
- Replies: 4
- Forum: Quantum Physics
-
S
Undergrad Normal distribution curve area?
Is there a relatively simple algorithm to compute the area in percentage under the curve as represented by a sigma value? For example; 3 sigma = 99.7 2 sigma = 95 1 sigma = 68.3 Now suppose I wanted to know 2.5 sigma without a table.- Scott S
- Thread
- Area Curve Distribution Normal Normal distribution
- Replies: 2
- Forum: Set Theory, Logic, Probability, Statistics
-

Calculating current distribution in a HF coaxial cable?
Hello, I would like to calculate the current distribution in a coaxial cable where the skin effect is significant. I asked this question on stackexchange and I provided pictures and more details there...- Cedric Eveleigh
- Thread
- Cable Coaxial Coaxial cable Current Current density Distribution Skin effect Transmission line
- Replies: 5
- Forum: Electrical Engineering
-
J
Graduate Distribution of Non-Gaussian Data: Analysis & Presentation
Any help would be much appreciated. The problem lies in the non-Gaussian distribution of the sample. If we take the entire data set of total fish catch, the skewness statistic equals 7.463 with a std. error of skewness of 0.39. Accordingly, the Z dist. (7.463/0.39)=19.14. Overall, the...- JohnFishy
- Thread
- Data Distribution Mean Non uniform Skew symmetric Standard deviation
- Replies: 3
- Forum: Set Theory, Logic, Probability, Statistics
-
W
Help understanding a set and its distribution
Homework Statement given set C = {(x,y)|x,y are integers, x^2 + |y| <= 2} Suppose they are uniformly distributed and we pick a point completely at random, thus p(x,y)= 1/11 Homework Equations Listing it all out, R(X) = {-1,-2,0,1,2} = R(y) The Attempt at a Solution My problem is that when I...- whitejac
- Thread
- Distribution Probability Set Sets Statistics Uniformity
- Replies: 2
- Forum: Precalculus Mathematics Homework Help
-
T
Sampling Distribution of Mean for Discrete Uniform Distribution with Replacement
Homework Statement suppose that 50 random samples of size n = 10 are to be taken from a population having the discrete uniform distribution f(x) = 1/10 for x = 0,1,2,...,9 0 elsewhere sampling is with replacement so that we are sampling from an infinite population. we get 50 random...- toothpaste666
- Thread
- Distribution Mean Sampling
- Replies: 12
- Forum: Calculus and Beyond Homework Help
-

Graduate Depiction of distribution of photons over time
I have a question about photons and the Schrödinger equation. Photons behave like particles but also as waves. I understand that this can be described by the Schrödinger equation as a photon having a certain probability to be somewhere. If I understand this correctly, I take it that there are...- entropy1
- Thread
- Distribution Particle Photon Photons Schrödinger Schrodinger equation Time Wave
- Replies: 3
- Forum: Quantum Physics
-
I
Undergrad Thermal energy distribution of an object?
Hey all, I just wanted confirmation. The thermal energy distribution of molecules in a system corresponds directly to its blackbody curve right?- iScience
- Thread
- Distribution Energy Thermal Thermal energy
- Replies: 1
- Forum: Thermodynamics
-

What is the Net Force on Charge Q1 in a Right Triangle Configuration?
Homework Statement A triangle is given with the points: Q1 = +2.0 x 10-5 C 2.0 m from Q3 = -3.0 x 10-5 C AND Q1 = +2.0 x 10-5 C 2.0 m from Q2 = -3.0 x 10-5 CThe triangle is a right triangle, with Q1 at the 90 degree angle.FIND THE NET FORCE OF CHARGE 1Homework Equations [/B] FE21 = FE31...- Dodsy
- Thread
- Charge Charge distribution Charges Distribution
- Replies: 11
- Forum: Introductory Physics Homework Help
-
C
Understanding Probability and Observations in Statistics
The assignment was already turned in a while ago, but I am currently reviewing all the past homework and trying to resolve the problems I couldn't understand. The website software gives the correct multiple choice or numerical answer, but not the steps. They gave me a weird answer and I didn't...- Callix
- Thread
- Distribution Hypergeometric Statistics
- Replies: 7
- Forum: Precalculus Mathematics Homework Help
-
P
Distribution of charge in hydrogen atom
Suppose the hydrogen atom consists of a positive point charge (+e), located in the center of the atom, which is surrounded by a negative charge (-e), distributed in the space around it. The space distribution of the negative charge changes according to the law p=Ce^(−2r/R), where C is a...- Peter Velkov
- Thread
- Atom Charge Distribution Electrostatic field Hydrogen Hydrogen atom
- Replies: 7
- Forum: Advanced Physics Homework Help
-
T
A normal distribution of IQ scores
Homework Statement It is known that the IQ score of ten-year-old children in a particular population has a normal distribution with mean 100 and standard deviation 15. (a) What proportion of this population have an IQ score above 115? (b) Mary’s IQ is equal to the 80th percentile of this...- toothpaste666
- Thread
- Distribution Iq Normal Normal distribution
- Replies: 6
- Forum: Calculus and Beyond Homework Help
-
T
Joint probability distribution
Homework Statement 4. Let X and Y have the joint probability distribution (a) Find P(X +Y ≤ 4). (b) Find the marginal probability distributions f1(x) and f2(y). (c) Find P(X < 2|Y = 2). (d) Are X and Y independent? The Attempt at a Solution a) f(1,1) + f(1,2) + f(1,3) + f(2,1) + f(2,2) +...- toothpaste666
- Thread
- Distribution Joint Probability Probability distribution
- Replies: 2
- Forum: Calculus and Beyond Homework Help
-
T
Solving Poisson Distribution Problems: Questions on Calls/Minute
Homework Statement A telephone operator receives four phone calls in three minutes on the average. Let a Poisson random number X denote the number of phone calls per minute to this operator. (a) Find the probability that this operator receives two phone calls in a minute. (b) Find the...- toothpaste666
- Thread
- Distribution Poisson Poisson distribution
- Replies: 2
- Forum: Calculus and Beyond Homework Help
-
T
Binomial distribution of coin tosses
Homework Statement 1. A fair coin is tossed 100 times. (a) Find an approximate probability of getting at least 60 heads. (b) Find an approximate probability of getting exactly 60 heads. The Attempt at a Solution part b) would be b(60;100,.5) part a) we would need the table for the cumulative...- toothpaste666
- Thread
- Binomial Binomial distribution Distribution
- Replies: 4
- Forum: Calculus and Beyond Homework Help
-

Binomial -> Poisson distribution question
Homework Statement A teacher has an infinite flow of papers to mark. They appear in his office at random times, at an average rate of 10 a day. On average 10% of the manuscripts are free from errors. What is the probability that the teacher will see exactly one error-free manuscript (a) after...- sunrah
- Thread
- Binomial Distribution Poisson Poisson distribution
- Replies: 10
- Forum: Calculus and Beyond Homework Help
-
C
Independent Process Probability distribution
A manufacturer has designed a process to produce pipes that are 10 feet long. The distribution of the pipe length, however, is actually Uniform on the interval 10 feet to 10.57 feet. Assume that the lengths of individual pipes produced by the process are independent. Let X and Y represent the...- carl123
- Thread
- Distribution Independent Probability Probability distribution Process Statistics Uniform
- Replies: 10
- Forum: Calculus and Beyond Homework Help
-
S
Electric Field: Continuous Charge Distribution
Homework Statement A nonconducting sphere 1.3 m in diameter with its center on the x axis at x = 4 m carries a uniform volume charge of density ρ = 4.8 µC/m3. Surrounding the sphere is a spherical shell with a diameter of 2.6 m and a uniform surface charge density σ = -1.2 µC/m2. Calculate the...- sxal96
- Thread
- Charge Charge distribution Continuous Continuous charge distribution Distribution Electric Electric field Field
- Replies: 12
- Forum: Introductory Physics Homework Help
-
T
Discrete probability distribution
Homework Statement 1. Consider selecting at random a student who is among the 15,000 registered for the current semester at a school Let X be the number of courses for which the selected student is registered and suppose that X has probability distribution x: 1 2 3 4 5 6...- toothpaste666
- Thread
- Discrete Distribution Probability Probability distribution
- Replies: 8
- Forum: Calculus and Beyond Homework Help
-
T
What is the probability of passing a shipment using a binomial distribution?
Homework Statement A company is interested in evaluating its current inspection procedure on large shipments of identical items. The procedure is to take a sample of 5 items and pass the shipment if no more than 1 item is found to be defective. It is known that items are defective at a 10%...- toothpaste666
- Thread
- Binomial Binomial distribution Distribution
- Replies: 2
- Forum: Calculus and Beyond Homework Help
-

Graduate Probability Distribution in Ensembles: Explained
I am confused about the basic idea of probability distribution in ensembles. Given macroscopic properties of the system, a system can have large number of micro states. But isn't the probability of finding a system in any of the micro state is equal? What is then the interpretation of this...- CassiopeiaA
- Thread
- Distribution Statistical mechanics
- Replies: 4
- Forum: Atomic and Condensed Matter
-
T
Exponential distribution problem
Homework Statement The amount of time that a surveillance camera will run without having to be reset is a random variable having the exponential distribution with beta = 50 days. find the probabilities that such a camera will a) have to be reset in less than 20 days b) not have to be reset in...- toothpaste666
- Thread
- Distribution Exponential Exponential distribution
- Replies: 6
- Forum: Calculus and Beyond Homework Help
-
D
Graduate When/how to reject Poisson distribution hypothesis?
Homework Statement I have run into a situation that my gut tells me is impossible (alright extremely unlikely) when assuming a Poisson distribution. I want to make this gut feeling more formal by testing it against a Poisson distribution. Sadly I'm not a schooled statistician. Generalised...- DaanV
- Thread
- Distribution Poisson Poisson distribution
- Replies: 15
- Forum: Set Theory, Logic, Probability, Statistics
-
R
Graduate Why do the energy levels in electronic band structures start at negative values?
In the graphs that I see around the internet I see that the energy axis starts at 0 eV and it goes up. So the electrons have positive energies. But in the electronic band structure, the electrons have negative energies. And if they go to infinity, then their energy becomes 0. So, what is...- RaduAndrei
- Thread
- Distribution Fermi-dirac Fermi-dirac distribution
- Replies: 5
- Forum: Atomic and Condensed Matter
-
C
Poisson Probability Distribution Problem
Homework Statement An article suggests that a Poisson process can be used to represent the occurrence of structural loads over time. Suppose the mean time between occurrences of loads is 0.4 year. a). How many loads can be expected to occur during a 4-year period? b). What is the probability...- Callix
- Thread
- Distribution Poisson Probability Probability distribution Statistics
- Replies: 19
- Forum: Precalculus Mathematics Homework Help
-
T
MHB Standard normal distribution probability
"A study of long distance phone calls made from the corporate offices of the Pepsi Bottling Group Inc. showed the calls follow the normal distribution. The mean length of time per call was 4.2 minutes and the standard deviation was 0.60 minutes. a.What is the probability the calls lasted...- trastic
- Thread
- Distribution Normal Normal distribution Probability Standard
- Replies: 1
- Forum: Set Theory, Logic, Probability, Statistics
-
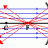
Graduate Average Speed for Maxwell's Distribution of Molecular Speed
Using the Maxwell-Boltzmann equation above, there is an example in my book (Giancoli 4th edition p. 481) where they use this to find the average velocity. I understand that it would just be the sum of all the speeds of the molecules divided by the number of molecules. But then I'm having...- RaulTheUCSCSlug
- Thread
- Average Average speed Boltzmann distribution Distribution Integration by parts Maxwell boltzmann Molecular Speed
- Replies: 2
- Forum: Electromagnetism
-
R
Undergrad Lorentz Transforms & Distribution Funcs: Physics Intro Help
Hi there, kinda new here so please let me know if this question has been answered. I am hoping to get a link or two to some good sources of information on Lorentz transforms and distribution functions (as used in physics). I understand DF's in class and I understand the math behind them I just...- Reed Kartye
- Thread
- Distribution Distribution function Functions Lorentz Lorentz transformation
- Replies: 4
- Forum: Special and General Relativity
-
F
Graduate QM probability and normal distribution
Is there a relationship between QM probability and normal distribution ? I'm thinking about drawing probability densities as functions of phase. Thanks- forcefield
- Thread
- Distribution Normal Normal distribution Probability Qm
- Replies: 17
- Forum: Quantum Physics
-
V
Distribution of charge on two spheres
Homework Statement Homework EquationsThe Attempt at a Solution I believe the entire charge Q has to be given to any of the sphere such that one charge is neutral ,while the other has charge Q . In this way there would be no electric force between the two spheres and only attractive force...- Vibhor
- Thread
- Charge Distribution Spheres
- Replies: 3
- Forum: Introductory Physics Homework Help
-
D
Megger Testing on Distribution Transformers
In Megger testing distribution transformers, how much importance is there in including the LV/HV bushings in the test. If you disconnect and have high readings independent of the bushing, and then put the bushings back into the circuit and the readings fall dramatically, what is that saying...- Dante Heater
- Thread
- Distribution Testing Transformers
- Replies: 5
- Forum: Electrical Engineering
-

Consider the Gaussian Distribution....?
Homework Statement Consider the Gaussian Distribution ## p(x) = Ae^{-\lambda(x-a)^{2}} ##, where ## A ##, ##a##, and ##\lambda## are constants. (Look up any integrals you need.) (a) Determine ##A## (I only need help with this (a)) Homework Equations ##\int_{-\infty}^{\infty} p(x)dx = 1##...- Destroxia
- Thread
- Distribution Gaussian Gaussian distribution
- Replies: 4
- Forum: Calculus and Beyond Homework Help
-
T
Lognormal distribution question
1. The lognormal distribution is identified as a model for concentration of a certain organic matter above a certain stretch of a highway. The parameters of this distribution are sigma = 1.9 and sigma = 0.9. a) Determine the expected value and the standard deviation of such distribution. b) The...- TooTall65
- Thread
- Distribution
- Replies: 3
- Forum: Calculus and Beyond Homework Help
-
T
Graduate Comparing gaussian distributions with Gumbel-like distribution
Hi all, I study binding of analytes in a platform where I have 10.000 sensors. there's is one binding event per sensor and I identify it as a sudden positive change in the signal. I do first a control experiment without analytes. I measure the maximum change in the signal for each sensor and I...- TryingTo
- Thread
- Distribution Distributions Gaussian
- Replies: 1
- Forum: Set Theory, Logic, Probability, Statistics
-
D
Power Distribution Design -- why did the person get shocked?
Hello I am an electrical engineer freshly out of school and i was wondering if anyone could help me reach an answer to this design problem. I am attempting this problem solely for personal knowledge because in school I never took a course on distribution design. I found this problem looking...- Derill03
- Thread
- Design Distribution Power
- Replies: 10
- Forum: Engineering and Comp Sci Homework Help
-
Z
Graduate Why wavefunction is not seen as substance distribution?
Why wavefunction (the square of its modulus) of an electron is not seen as a measure of substance/charge distribution of the electron?- zhanhai
- Thread
- Distribution Wavefunction
- Replies: 6
- Forum: Quantum Physics
-
M
MHB Normal distribution question: determine sigma
The lengths of a certain species of worm follow a normal distribution. Thirty percent of the worms are at least 16cm long, and 15% of the worms are less than 10cm long. Find, to 2 decimal places, the standard deviation of the lengths of the worms.- muffymuff
- Thread
- Distribution Normal Normal distribution Sigma
- Replies: 2
- Forum: Set Theory, Logic, Probability, Statistics
-

Graduate Distribution of the zeros of the zeta function
In http://www.americanscientist.org/issues/pub/the-spectrum-of-riemannium/5, the author mentions that the function P(x) = 1-(sin(πx)/(πx))2 seems to be, assuming the Riemann Hypothesis is true, to the two-point correlations of the zeros of the Riemann zeta function. Going by...- nomadreid
- Thread
- Distribution Function Zeta function
- Replies: 3
- Forum: Set Theory, Logic, Probability, Statistics
-
V
MHB Computing joint cumulative distribution function
With X having the exponential $(\lambda)$ distribution and $Y = X^3$, how do I compute the joint cumulative distribution function? Here is how far I've come: $F(x,y) = P(X ≤ x, Y ≤ y) = P(X ≤ x, x^3 ≤ y) = P(X ≤ x, X ≤ y^{1/3}) = P(X ≤ min(x, y^{1/3})$, $f_x(x) = \lambda e^{-\lambda x}$$ for...- vincentvance
- Thread
- Computing Distribution Distribution function Function Joint
- Replies: 1
- Forum: Set Theory, Logic, Probability, Statistics