Function Definition and 1000 Threads
-

The given function is an even or an odd function?
I think the answer is an even function as the function ##x^2## is an even function and thus, is symmetrical w.r.t. Y axis. The question I have is how to do this problem algebraically. I tried to graph some functions on GeoGebra to verify my answer. a) ##y = ln(x^2)## b) ##y = sin(x^2)##...- brochesspro
- Thread
- Algebra even Function Pre calculus Pre-calculus Precalculus
- Replies: 11
- Forum: Precalculus Mathematics Homework Help
-
D
Compute the residue of a function
There is a typo. It should say ##h=\frac{f}{g}##. Attempt: ##f## and ##g## are holomorphic on ##\Omega##. Homomorphic functions form a ##\mathcal{C}^*## algebra, so ##h## is holomorphic on ##\Omega## where ##g\neq 0##. If ##z_0## is a removal singularity of ##h##, then ##Res(h,z_0)=0## by...- docnet
- Thread
- Function Residue
- Replies: 2
- Forum: Calculus and Beyond Homework Help
-

Designing a ripple low PS for DDS function generator
Hello to all. I am trying to design a ripple free (read as ripple free as possible) power supply (PS) for my DIY DDS function generator. I am (was) in the possession of the hyland 5v to 12v PS which wrecked due to a stupid action on my side, my bad. so i was going to repair it, but i found that...- matthieu1973
- Thread
- Designing Function Function generator Generator Ripple
- Replies: 6
- Forum: Electrical Engineering
-
L
Can Cauchy's Residue Theorem be Used for Functions with Branch Cuts?
First of all I am not sure which type of singularity is ##z=0##? \ln\frac{\sqrt{z^2+1}}{z}=\ln (1+\frac{1}{z^2})^{\frac{1}{2}}=\frac{1}{2}\ln (1+\frac{1}{z^2})=\frac{1}{2}\sum^{\infty}_{n=0}(-1)^{n}\frac{(\frac{1}{z^2})^{n+1}}{n+1} It looks like that ##Res[f(z),z=0]=0##- LagrangeEuler
- Thread
- Complex Complex function Function Residue
- Replies: 12
- Forum: Calculus and Beyond Homework Help
-
D
Undergrad What is the ambiguity in forming new functions?
Why do we want to always deal with single valued functions? In the classical treatment a function is a rule which assigned to one number another number. In the modern sense, it is a rule which assigns to each element in a set called the domain an element (one element) in a set called the range...- DumpmeAdrenaline
- Thread
- Definition Function
- Replies: 28
- Forum: Calculus
-
H
Angular momentum of the particle about point P as a function of time
I don't understand why my solution is wrong. Here is my solution. $$ r_{\theta} = R\cos{\theta} \vec{i} + R\sin{\theta} \vec{j} $$ $$ v_{\theta} = v\cos(\theta + \frac{\pi}{2}) \vec{i} + v\sin(\theta + \frac{\pi}{2}) \vec{j} $$ $$ p_{\theta} = mvR(-\sin{\theta}) \vec{i} +mvR(\cos{\theta}...- hhjjy
- Thread
- Angular Angular momentum Function Momentum Particle Point Time
- Replies: 13
- Forum: Introductory Physics Homework Help
-
D
True or false? |z|^2 is an entire function
False The reasoning for answer: The absolute value function is is not analytic wherever its argument equals zero. ##f## is not analytic at ##z=0## so it is not entire.- docnet
- Thread
- Function
- Replies: 16
- Forum: Calculus and Beyond Homework Help
-

Finding the horizontal shift of a function
I've never actually done this, so I was wondering if someone could show me how this is done. One way I tried was by simply using ##cos^{-1}## in order to cancel the cosine, but that gave me a different value, so I assume this is not how you are supposed to do this. --> I know I am supposed to...- Einstein44
- Thread
- Function Horizontal Shift
- Replies: 10
- Forum: Precalculus Mathematics Homework Help
-

Fog Droplet Size as a function of Ultrasound Frequency
I need to know how to predict particle size of a water driplet produced by a given ultrasonic frequency? For example, an ultrasonic fogger will create ~5 micron water driplets at a frequency of 1.75 MHz. I do know that the higher the frequency the smaller the driplet diameter. How is this...- Moondog
- Thread
- Frequency Function Ultrasound
- Replies: 6
- Forum: Mechanical Engineering
-

Undergrad Describing homeomorphisms with the π1 function
Here is what the problem looks like. The thing is I don't remember what π1is exactly and I don't really know much group theory or know what equivalence classes are. I remember learning some group theory fact that f*(n) = n*f*(1). So, I think (a) was just equal to m since f(1) = 1 and (b) was...- Mikaelochi
- Thread
- Function
- Replies: 2
- Forum: Topology and Analysis
-
J
High School Is there a function for every possible "path"?
Has any path/line/shape/contour function? And how find function of complex "path"? for example this?- Jurgen M
- Thread
- Function Path
- Replies: 19
- Forum: Topology and Analysis
-

Problem when std::function refers to member function
Hi, I have a class master_t which is composed by two other classes, dev_a, dev_b. I would like that a member function from the dev_b object (within master_t) could use a member function of dev_a object (within master_t). This is a minimal working code, where line 26 implements this feature...- ORF
- Thread
- Function Member
- Replies: 2
- Forum: Programming and Computer Science
-
C
Undergrad What's the definition of "periodic extension of a function"?
I'm learning about Fourier theory from my lecture notes and I have a few questions that I wasn't able to concretely find answers to: 1. What's the definition of periodic extension? I think the definition is as follows ( Correct me if I'm wrong please ): for ## f: [ a,b) \to \mathbb{R} ## its...- CGandC
- Thread
- Definition Extension Fourier Function Periodic Real analysis
- Replies: 14
- Forum: Topology and Analysis
-

Quartic function of a non-ideal spring
I'm stuck in a part of my problem where I need to find the roots of this function which represent turning points for a non-ideal spring.- Semiclassical
- Thread
- Function Polynomial Spring Spring energy
- Replies: 1
- Forum: Introductory Physics Homework Help
-
Z
Spivak, Ch. 5 Limits, Problem 3 viii: Prove a limit of a function
Consider item ##vii##, which specifies the function ##f(x)=\sqrt{|x|}## with ##a=0## Case 1: ##\forall \epsilon: 0<\epsilon<1## $$\implies \epsilon^2<\epsilon<1$$ $$|x|<\epsilon^2\implies \sqrt{|x|}<\epsilon$$ Case 2: ##\forall \epsilon: 1\leq \epsilon < \infty## $$\epsilon\leq\epsilon^2...- zenterix
- Thread
- Calculus Function Limit Limit definition Limits Spivak
- Replies: 16
- Forum: Calculus and Beyond Homework Help
-
D
Prandtl stress function for circular bar in torsion
For a Prandtl stress function to be valid, it must be zero on the boundary. For a circular bar, both of these work: $$\phi_1 = C\left(\frac{x^2}{r^2}+ \frac{y^2}{r^2} - 1\right)$$ $$\phi_2 = C \left(x^2+ y^2- r^2\right)$$ But performing the integration for the internal torque M gives...- davidwinth
- Thread
- Circular Function Stress Torsion
- Replies: 2
- Forum: Mechanical Engineering
-
D
Find the Laurent Series of a function
(a) i tried to decompose the fracion as a sum of fractions of form ##\frac{1}{1-g}## $$f=\frac{-z}{(1+z)(2-z)}=\frac{a}{1+z}+\frac{b}{2-z}$$ $$a=\frac{1}{3}, b=-\frac{2}{3}$$ $$f=\frac{1}{6}\frac{1}{1+z}-\frac{1}{3}\frac{1}{1-\frac{z}{2}}$$ $$f=\frac{1}{6}\sum_{n=0}^\infty...- docnet
- Thread
- Function Laurent series Series
- Replies: 9
- Forum: Calculus and Beyond Homework Help
-
D
Find the order of the pole of a function
I learned that ##f## has another singular point at ##z=1.715##, but i don't think this would be related to the pole at ##z=0## I tried substitutine ##u=2\cos z-2+z^2## and $$f(u)=\frac{1}{u^2}$$ has a pole of order 2 at ##u=0## which happens i.f.f. ##z=0## or ##z=1.715##. so ##f## has a pole...- docnet
- Thread
- Function Pole
- Replies: 9
- Forum: Calculus and Beyond Homework Help
-
C
Undergrad Finding a Rational Function with data (Pade approximation)
Dear Everybody, I need some help understanding how to use pade approximations with a given data points (See the attachment for the data). Here is the basic derivation of pade approximation read the Derivation of Pade Approximate. I am confused on how to find a f(x) to the data or is there a...- cbarker1
- Thread
- Approximation Data Data sets Function Numerical approximation Rational
- Replies: 4
- Forum: MATLAB, Maple, Mathematica, LaTeX
-
H
Potential energy, Wave function, Quantum physics
I am totally confused about the task. Any help will be nice. Thank you so much- HektorHusky
- Thread
- Energy Function Physics Potential Potential energy Quantum Quantum physics Wave Wave function
- Replies: 1
- Forum: Introductory Physics Homework Help
-
T
Graduate When KE is a function of position
Hi all In the Lagrangian, we have L = KE - PE In most cases, I have seen KE as a function of q and q-dot (using the generic symbols). However I first learned how KE = 0.5 m * v-squared. Later, I used generalized coordinates and THAT is when KE became a function of q. I get all that...- Trying2Learn
- Thread
- Function Position
- Replies: 2
- Forum: Mechanics
-
M
Mathematica Fitting solution function of NDSolve with a curve
The following solves an IVP, giving the output as the function f3[x]: s3 = NDSolve[{(-z1[t]^(3/2) + (1 + z1[t]^2)^(3/4))/( 3 (-z1[t] + Sqrt[1 + z1[t]^2])) == z1[t] z1'[t], z1[0] == 0.0001}, z1, {t, 0, 30} f3[x_] := z1[x] /. First[s3]; My question is, how do I curve fit f3[x] to the...- member 428835
- Thread
- Curve Fitting Function
- Replies: 1
- Forum: MATLAB, Maple, Mathematica, LaTeX
-
P
Proof that given function is convex
Part 1 ##\left\| \vec{y} \right\|^2 \leq \left\| \vec{y} \right\|^2## and since ##\lambda \in \left[ 0,1 \right] \Rightarrow \lambda^2 \leq \lambda## So ##\lambda^2 \left\| \vec{y} \right\|^2 \leq \lambda \left\| \vec{y} \right\|^2 ## Part 2 ##\left\| \vec{x} \right\|^2 \leq \left\| \vec{x}...- PhDeezNutz
- Thread
- Convex Function Proof
- Replies: 9
- Forum: Calculus and Beyond Homework Help
-
S
Undergrad How to Find the Derivative of F = f(x)/f(x+dx)?
Hello, I'm struggling with this for some time. So I have the function: f(x) = sqrt(1 - 1/x) The derivative of this function can be easily calculated. Now we define the function: F(x) = f(x)/f(x + dx) = sqrt(1 - 1/x)/sqrt(1 - 1/(x+dx)) I have a hard time to find F'(x) due to the presence of... -
R
Undergrad Finding the maximum of a function
Why does f attain its local maximum at r' in (p,q). Is it because we have f(x)<= f(r') for all x in (p,p+delta)? -
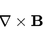
Delta function to calculate density of probablity
- anaisabel
- Thread
- Advance physics Delta Delta function Density Density function Function
- Replies: 9
- Forum: Advanced Physics Homework Help
-
Z
How to choose the correct function to use for a Taylor expansion?
Consider two different Taylor expansions. First, let ##f_1(s)=(1+s)^{1/2}## $$f_1'(s)=-\frac{1}{2(1+s^{3/2})}$$ Near ##s=0##, we have the first order Taylor expansion $$f_1(s) \approx 1 - \frac{s}{2}$$ Now consider a different choice for ##f(s)## $$f_2(s)=(1+s^2)^{1/2}$$...- zenterix
- Thread
- Electromagnetism Expansion Function Taylor Taylor expansion
- Replies: 7
- Forum: Introductory Physics Homework Help
-

Line integral of a scalar function about a quadrant
[FONT=times new roman]Problem : [FONT=times new roman]We are required to show that ##I = \int_C x^2y\;ds = \frac{1}{3}##. Attempt : Before I begin, let me post an image of the problem situation, on the right. I would like to do this problem in three ways, starting with the simplest way - using...- brotherbobby
- Thread
- Cartesian coordinates Contour integral Function Integral Line Line integral Scalar
- Replies: 4
- Forum: Calculus and Beyond Homework Help
-

Undergrad A function with no max or min at an endpoint
Hi, PF Although a function cannot have extreme values anywhere other than at endpoints, critical points, and singular points, it need not have extreme values at such points. There is an example of how a function need not have extreme values at a critical point or a singular point in 9th edition...- mcastillo356
- Thread
- Function Max
- Replies: 7
- Forum: Calculus
-
R
Fourier series, periodic function for a string free at each end
From the statement above, since the ring is massless, there's no force acting vertically on the rings. Thus, the slope is null. ##\frac{\partial y(0,0)}{\partial x} = \frac{\partial y(L,0)}{\partial x} = 0## ##\frac{\partial y(0,0)}{\partial x} = A\frac{2 \pi}{L}cos(\frac{2 \pi 0}{L}) =...- Redwaves
- Thread
- Fourier Fourier series Function Periodic Periodic functions Series String
- Replies: 8
- Forum: Introductory Physics Homework Help
-

Undergrad Writing the wave function solutions for a particle in a 2-D box
The final wave function solutions for a particle trapped in an infinite square well is written as: $$\Psi(x,t) = \Sigma_{n=1}^{\infty} C_n\sqrt{\frac{2}{L_x}}sin(\frac{n\pi}{L_x}x)e^{-\frac{in^2{\pi}^2\hbar t}{2m{L_x}^2}}$$ The square of the coefficient ##C_n## i.e. ##{|C_n|}^2## is...- Hamiltonian
- Thread
- Box Function Particle Wave Wave function Writing
- Replies: 1
- Forum: Quantum Physics
-

Undergrad Plasmonic - Dielectric function
Regarding the electrical permittivity of the metal in a high frequency regime, I cannot find research material related to the lead dielectric function (PD). I can't get the matatrial as values, I'll let you comment on that. I know that Pd can inhibit the amount of gamma rays in the x-ray case...- LUFER
- Thread
- Dielectric Function
- Replies: 4
- Forum: Quantum Physics
-
P
Graduate $\phi^4$ in $4 - \epsilon$ dimension renormalization beta function
Hi all, I am currently studying renormalization group and beta functions. Since I'm not in school there is no one to fix my mis-understandings if any, so I'd really appreciate some feedback. PART I: I wrote this short summary of what I understand of the beta function: Is this reasoning...- paralleltransport
- Thread
- Beta Beta function Dimension Epsilon Function Renormalization
- Replies: 2
- Forum: High Energy, Nuclear, Particle Physics
-
L
Undergrad Second derivative of chained function
Let's say we have a function ##M(f(x))## where ##M: \mathbb{R}^2 \to \mathbb{R}^2## is a multivariable linear function, and ##f: \mathbb{R} \to \mathbb{R}^2## is a single variable function. Now I'm getting confused with evaluating the following second derivative of the function: $$ [M(f(x))]''... -

Checking if a function is an equipotential surface
hi guys I came across that theorem that could be used to check if a surface represented by the function f(x,y,z) = λ could represent an equipotential surface or not, and it states that if this condition holds: $$\frac{\nabla^{2}\;f}{|\vec{\nabla\;f}|^{2}} = \phi(\lambda)$$ then f(x,y,z) could...- patric44
- Thread
- equipotential Function Potential Surface
- Replies: 3
- Forum: Advanced Physics Homework Help
-

An expression for the vertical velocity as a function of time
A rocket of initial mass m0 is launched vertically upwards from the rest. The rocket burns fuel at the constant rate m', in such a way, that, after t seconds, the mass of the rocket is m0-m't. With a constant buoyancy T, the acceleration becomes equal to a=T/(m0-m't) -g. The atmospheric...- Physil
- Thread
- Expression Function Time Velocity Vertical Vertical velocity
- Replies: 5
- Forum: Introductory Physics Homework Help
-
S
MHB Interpolating Points with Continuous Modular Functions?
Define a continuous function $$F(x;n)$$ that interpolates points (x, x mod n) for a given integer n and all integer x. For example $$F(x;2)=\frac{1}{2}-\frac{1}{2}\cos\left(\pi x\right)$$ interpolates all points (x, x mod 2) when x is an integer. Similarly $$F(x;3)$$ should interpolate points...- SatyaDas
- Thread
- Continuous Function
- Replies: 5
- Forum: General Math
-

Transfer function with initial conditions (DE)
I have a differential equation of the form y''(t)+y'(t)+y(t)+C = 0. I think this implies that there are non-zero initial conditions. Is it possible to write a transfer function for this system? This post...- MechEEE
- Thread
- Conditions Function Initial Initial conditions Transfer function
- Replies: 8
- Forum: Calculus and Beyond Homework Help
-

Engineering Electrical and Control Engineering: Transfer Function Reduction problem
- AncientOne99
- Thread
- Control Control engineering Electrical Engineering Function Reduction Transfer function
- Replies: 24
- Forum: Engineering and Comp Sci Homework Help
-
S
Using the sin function for a problem with a frictionless pulley and an incline
To find the tension in the rope connecting 6.0 kg block and 4.0 kg block we do 6.0 kg = m1, 4.0 kg = m2, 9.0 kg = M (m_2 + m_1)a - Ma = Mg - m_2 gsin\theta - m_1 gsin\theta Why do we use sin in these equations and not cos?- sentimentaltrooper
- Thread
- Frictionless Frictionless pulley Function Incline Pulley Sin
- Replies: 8
- Forum: Introductory Physics Homework Help
-
D
Prove that a function from [0,1] to [0,1] is a homeomorphism
let ##X=\{0,p1,p_2,...,p_n,1\}## and ##Y=\{0,p1,p_2,...,p_n,1\}## be sets equipped with the discrete topology. for each ##q_i## in ##Y##, the inverse image ##h^{-1}(q_i)=p_i## is open in ##X## w.r.t. to the discrete topology, so h is continuous. every element y in Y has a preimage x in X, so h...- docnet
- Thread
- Function Homeomorphism
- Replies: 5
- Forum: Calculus and Beyond Homework Help
-
D
Prove that the concatenation function is continuous
Let f be continuous in [0,1] and g be continuous in [1,2] and f(1)=g(1). prove that $$ (f*g)= \begin{cases} f(t), 0\leq t\leq 1\\ g(t), 1\leq t \leq2 \end{cases}$$ is continuous using the universal property of quotient spaces. Let ##f:[0,1]→X## and ##g:[1,2]→Y## f and y are continuous, thus...- docnet
- Thread
- Continuous Function
- Replies: 12
- Forum: Calculus and Beyond Homework Help
-

Undergrad Doing proofs with the variety function and the Zariski topology
I included this image because it is easier than typing it out. Anyway, this is an old problem I need to catch up on. I have a clue as to how to do part a. I could say given an x that is a member of ∩V(Ai) which implies that x is a member of V(Ai) for ∀i. Then we can say ∀i all polynomials are in...- Mikaelochi
- Thread
- Function Proofs Topology
- Replies: 5
- Forum: Topology and Analysis
-
M
Graduate Array variable of envelope function (parameter representation)
Hi, I have a question regarding the envelope function in parameter representation. Let an array of curves in cartesian coordinates be given in parameter representation, with curve parameter 𝑡 and array variable 𝑐 𝑥=𝑥(𝑡,𝑐) 𝑦=𝑦(𝑡,𝑐) Condition for envelope is: 𝜕/𝜕𝑡 𝑥(𝑡,𝑐) 𝜕/𝜕𝑐 𝑦(𝑡,𝑐)=𝜕/𝜕𝑐...- mk3
- Thread
- Array Function Representation Variable
- Replies: 2
- Forum: Differential Geometry
-

Undergrad Question about Inverse Derivative Hyperbola function
Im confused about a certain part of solving an equation. So I used the hyerbola formula to find the answer but I think I did the math wrong. X^2-y^2=c^2 X=1 Y= (2x^5-1)^2 I did the calculations as you can see in the picture but I know I messed up on the square root part. When you square one... -
I
How can I plot the function g(x) = sin(πn/L) x and its corresponding g²(x)?
Summary:: We are currently studying basics of quantum mechanics. I'm getting the theory part but it's hard to visualise everything and understand. We are given this question to plot the function so if someone could help me in this. Plot the following function and the corresponding g²(x) g(x)...- Idonthave
- Thread
- Function Graph Plotting Wave Wave function Wavefunction
- Replies: 13
- Forum: Introductory Physics Homework Help
-

Find the intensity as function of y (interference between two propagating waves)
Let a spherical wave propagate from the origin, $y = ADcos(wt-2\pi r/ \lambda)/r$. Also, let a plane wave propagate parallel to the x axis, $y = Acos(wt-2\pi r/ \lambda)$. At x = D there is a flat screen perpendicular to the x axis. Find the interference at the point y on the screen as function...- LCSphysicist
- Thread
- Function Intensity Waves
- Replies: 3
- Forum: Introductory Physics Homework Help
-
Undergrad Which kind of function is this?
I'm curious how close someone could get to guessing the functions that generated the data shown below. And also, without looking at the plot, what do you think would be the most interesting looking function of x,y,z you can think of. A) B) C)- Jarvis323
- Thread
- Function
- Replies: 3
- Forum: General Math
-

Undergrad Proving a function f is continuous given A U B = X
Basically with this problem, I need to show that f is continuous if A and B are open and if A and B are closed. My initial thoughts are that in the first case X must be open since unions of open sets are open. My question is that am I allowed to assume open sets exist in Y? Because then I can...- Mikaelochi
- Thread
- Continuous Function
- Replies: 5
- Forum: Topology and Analysis
-
F
"Trick" for a specific potential function defined with an integral
Hello, To first clarify what I want to know : I read the answer proposed from the solution manual and I understand it. What I want to understand is how they came up with the solution, and if there is a way to get better at this. I have to show that, given a vector field ##F## such that ## F ...- fatpotato
- Thread
- Field Function Integral Multivariable calculus Potential Specific
- Replies: 10
- Forum: Calculus and Beyond Homework Help