What is generalized: Definition and 215 Discussions

A generalization is a form of abstraction whereby common properties of specific instances are formulated as general concepts or claims. Generalizations posit the existence of a domain or set of elements, as well as one or more common characteristics shared by those elements (thus creating a conceptual model). As such, they are the essential basis of all valid deductive inferences (particularly in logic, mathematics and science), where the process of verification is necessary to determine whether a generalization holds true for any given situation.
Generalization can also be used to refer to the process of identifying the parts of a whole, as belonging to the whole. The parts, which might be unrelated when left on their own, may be brought together as a group, hence belonging to the whole by establishing a common relation between them.
However, the parts cannot be generalized into a whole—until a common relation is established among all parts. This does not mean that the parts are unrelated, only that no common relation has been established yet for the generalization.
The concept of generalization has broad application in many connected disciplines, and might sometimes have a more specific meaning in a specialized context (e.g. generalization in psychology, generalization in learning).In general, given two related concepts A and B, A is a "generalization" of B (equiv., B is a special case of A) if and only if both of the following hold:

Every instance of concept B is also an instance of concept A.
There are instances of concept A which are not instances of concept B.For example, the concept animal is a generalization of the concept bird, since every bird is an animal, but not all animals are birds (dogs, for instance). For more, see Specialisation (biology).

View More On Wikipedia.org
Recent contents Top users
  1. T

    I Is F = ma the generalized force equation?

    It just seems odd that the force on an object goes based on the second time derivative of its position vector. I understand that this is what is observed through experiment, but is this only for certain types of situations? Is the acceleration only some kind of low-order approximation of a...
  2. O

    Questions regarding generalized work equation

    Hello, I am trying to generalize the work equation and understand the very definition of it. From what I understand, Work is the energy required to displace an object with a force in the direction of the displacement. (also the change in kinetic energy but I'm not going to worry about that yet)...
  3. H

    Why generalized force equals to zero?

    Homework Statement Lecturer says that: Generalized Coordinate: θ = q1 Generalized Force: Q1 = 0 I don't understand why Q1 equals to zero. Homework Equations Q_i = \sum_j \underline F_j \frac{\delta \underline r_j}{\delta q_i} The Attempt at a Solution First i need to find partial...
  4. Jianphys17

    Is there a generalized curl operator for dimensions higher than 3?

    Hi, i now studying vector calculus, and for sheer curiosity i would like know if there exist a direct fashion to generalize the rotor operator, to more than 3 dimensions! On wiki there exist a voice https://en.wikipedia.org/wiki/Curl_(mathematics)#Generalizations , but I do not know how you...
  5. Isaac0427

    Notation for generalized coordinates

    I have seen both rk and qj both used to represent generalized coordinates in the Lagrange equations. Are these both the same things? Does it matter which you use? Thanks!
  6. amjad-sh

    Calculating generalized force in two different ways

    Homework Statement a ladder of length L and mass m is leaning against a wall as shown in the figure below. assuming the wall and the floor are frictionless, the ladder will slide down the floor and until the left end loses contact with the wall. Before the ladder loses contact with the wall...
  7. S

    Generalized Coordinates - Landau & Lifshitz

    If suppose only if the velocities are determined for all N particles can the system be completely determined, can we not extend and say that only if acceleration for all particles are provided can the system be completely determined? For instance can there not be two systems of N particles with...
  8. O

    MHB Generalized triangle inequality in b-metric spaces

    How is the generalized triangle inequality in b-metric spaces ? I find something...But I wonder your opinion...Thank you for your attention... Especially if you write for n,m>0 m>n $d({x}_{n},{x}_{m})$$\le$..... I will be happy...
  9. P

    Generalized velocity addition and aberration formulas

    Not sure if this will be of interest to others, but, as an exercise, I decided to derive formulas for SR velocity addition for any angular relationship, and similar aberration of angle for any object speed and direction and observer relative velocity - using pure algebra/geometry. That is, no...
  10. Cosmophile

    Generalized Trigonometric Intervals

    Homework Statement Identify the intervals of increase/decrease of ##f(x) = \sin x + \cos x## Homework Equations ##f(x) = \sin x + \cos x## ##f'(x) = \cos x - \sin x = \sqrt 2 \cos(x+\frac {\pi}{4})## The Attempt at a Solution ##f## is increasing when ##f'(x) > 0## ##\sqrt 2 \cos(x+\frac...
  11. B

    Differentiate time derivative w/ respect to generalized var.

    Homework Statement Solve ∂v/∂θ and ∂v/∂r. (refer to attached image for equations) Homework Equations Refer to attached image. note that the velocity is expressed in cylindrical coordinates and attention must be paid to the directional unit vectors eθ and eρ.[/B] The Attempt at a Solution...
  12. kostoglotov

    Newton's Method generalized to 3 dimensions

    Homework Statement Prelim: my question is about a very specific part of a question whereby the student is asked to derive the final formula for the general solution in two vars, but I will post the entire question for clarify. Newton's Method for approximating the roots of an equation f(x)=0...
  13. gulfcoastfella

    Point of application of generalized forces of constraint

    In Lagrangian Dynamics, I assume that generalized forces of constraint are applied at the location of the corresponding generalized coordinate. I don't recall seeing anything explicit about the point of application in the text.
  14. Coffee_

    Mechanics, question about generalized coordinates

    I can start explaining the problem but a more quicker way would be to open this link: http://onlinelibrary.wiley.com/doi/10.1002/9783527627486.app2/pdf and check the paragraph resulting in expression (B.5). Note that I don't really care about the kinetic energy they talk about in this link...
  15. Legend101

    Integral involving Dirac Delta generalized function

    Homework Statement Evaluate the integrals in the attached image Homework EquationsThe Attempt at a Solution
  16. LarryS

    Generalized Dirac Equation for All Fermions?

    The original Dirac Equation was for the electron, a particle of spin 1/2. Is there a "Generalized Dirac Equation" that has been experimentally proven to work for all fermions, not just those of spin 1/2? Thanks in advance.
  17. evinda

    MHB Countable Union of Countable Sets

    Hello! (Wave) I am looking at the proposition: If $(A_n)_{n \in \omega}$ is a sequence of sets and $(f_n)_{n \in \omega}$ is a sequence of functions then: for all $n \in \omega, f_n: \omega \overset{\text{ surjective }}{\rightarrow} A_n$ then there is a function $f: \omega \overset{\text{...
  18. M

    MHB Generalized Holder Inequality: Proving the Inequality for Arbitrary Exponents

    Let $a_i \in \mathbb R^n$ with $a_i = (a_{i}^j)_{j = 1 ... n} = (a_{i}^1, ... ,a_{i}^n)$ for $i = 1, ... , k$ and let $p_1,...,p_k \in \mathbb R_{>1}$ with $\frac1{p_1}+ ... + \frac1{p_k} = 1$ Then show the following inequality by assuming that there are for every $i = 1, ... ,k$ one $N \in...
  19. G

    Skewed Generalized Gaussian Distribution

    I am looking for more information (e.g., reference, the CDF and descriptive stats) about a four-parameter skewed generalized Gaussian (SGG) distribution. I have come across the PDF for this distribution, but with no reference and not a lot of other information. Here is a snippet... On...
  20. R

    MHB Elementary proof of generalized power mean inequality

    This is problem 20b from chapter I 4.10 of Apostol's Calculus I. The geometric mean G of n positive real numbers x_1,\ldots, x_n is defined by the formula G=(x_1x_2\ldots x_n)^{1/n}. Let p and q be integers, q<0<p. From part (a) deduce that M_q<G<M_p when x_1,x_2,\ldots, x_n are not all...
  21. D

    Can I use generalized Stokes' theorem in Faraday's law?

    It is a nonsense use the generalized Stokes' theorem in right side of Faraday's Law? we know this is true...\displaystyle \oint_{\partial \Sigma}\vec{E}\cdot dl=-\int_{\Sigma} \frac{d\vec{B}}{dt}\cdot d\vec{A}\Rightarrow \int_{\Sigma}\vec{\nabla}\times\vec{E}\cdot d\vec{A}=-\int_{\Sigma}...
  22. P

    Center of Force, Generalized Potential

    The problem states that a particle moves in a plane under the influence of the following central force: F = \frac{1}{r^2}\Big(1 - \frac{\dot{r}^2 - 2\ddot{r}r}{c^2}\Big) and I am asked to find the generalized potential that results in such a force. Goldstein gives the following equation...
  23. Dale

    Coordinate Charts vs Generalized Coordinates

    When you have a general coordinate chart on spacetime you have a lot of freedom to pick your coordinates, but you are always going to have 4 coordinates and each 4-tuple uniquely (in that chart) identifies one event in the manifold. When you are choosing generalized coordinates for a...
  24. B

    A Generalized Quadratic Formula

    Just over two years ago, I was introduced to the process of completing the square as a way to solve the roots in a quadratic equation. More recently, I've thought about how I could go about extending this to completing the cube. The following short story/proof is the result of during just that...
  25. STEMucator

    Generalized Eigenvector Solutions for a System of Differential Equations

    Homework Statement Solve the system: ##x' = 5x - y## ##y' = 4x + y## Homework Equations ##t## is transpose. The Attempt at a Solution I'm a bit rusty with these and I had a small question. I put the system into the form ##x' = Ax## and proceeded to solve for the...
  26. L

    Generalized statistical interpretation

    I red griffiths many times but even now there is something I can't understand. It's about statistical interpretation. In his book chapter 3.4 he says "If you measure an observable Q(x,p) on a particle in the state ψ(x,t), you are certain to get one of the eigenvalues of the hermitian operator...
  27. M

    How to apply boundary condition in generalized eigenvalue problem?

    Hi all, Generally boundary condition (Dirichlet and Neumann) are applied on the Load Vector, in FEM formulation. The equation i solved, is Generalized eigenvalue equation for Scalar Helmholtz equation in homogeneous wave guide with perfectly conducting wall ( Kψ =λMψ ), and found, doesn't...
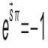
  28. Abel Cavaşi

    Generalized Helix: What Do You Think?

    What do you think, might be generalized the helix in the manner that I propose in the attached material?
  29. R

    Lighthill generalized function book

    Homework Statement see the pictures Homework EquationsThe Attempt at a Solution one. In the third picture. 3rd line and 4th line. i don't understand why 1-e^(-t^2/n^2) become (1+t^2)/n^2 two. I'm not familiar with proving equality by showing difference going to zero. for example, I prove...
  30. M

    Generalized Schrödinger equation

    This equation (see attachment) appears in one of Prof. Susskinds's lectures on Quantum Mechanics: in trying to differentiate the coefficients of the eigenvectors of a wave function with respect to time, an exponential e^(-iEt) is introduced for alpha. I can see that d/dt e^(-iEt) = -iE...
  31. D

    Generalized mathematical induction

    Recall that the fibonacci sequence is defined as { f0=0; f1 = 1 and {fn = f n - 1 + fn -2 for n 2 Prove by generalized mathematical induction that fn = 1/sqrt(5)[ϕn - (-ϕ)-n] where ϕ = [1+sqrt(5)]/2 is the golden ratio.. (This is known as de Moivre's formula.) So...
  32. mathbalarka

    MHB Generalized Erdos-Moser conjecture

    I have been researching on a generalization of Erdos-Moser, which asks for ordered tuple of consecutive integers with first $n-1$ integers, summed and exponentiation by $n$, equals the $n$-th power of the last and the greatest. The generalization can be observed as $$3^2 + 4^2 = 5^2$$ $$3^3 +...
  33. DreamWeaver

    MHB Generalized Log-Trig series related to the Hurwitz Zeta

    This thread is dedicated to the study of Log-Trig series of the form: \mathscr{S}_{(m, n)} (z) = \sum_{k=1}^{\infty}\frac{(\log k)^m}{k^n}\, \sin 2\pi k z\mathscr{C}_{(m, n)} (z) = \sum_{k=1}^{\infty}\frac{(\log k)^m}{k^n}\, \cos 2\pi k zWhere m, n \in \mathbb{Z} \ge 1, and 0 < z < 1 \in...
  34. DreamWeaver

    MHB Nielsen Polylogarithms and the Generalized Logsine Integral

    In this tutorial we will be exploring the Nielsen Polylogarithm, and it's close relative, the Generalized Logsine Integral. Both of these functions have numerous applications in maths and physics, not least of all in Quantum Theory. The main purpose here, however, will be employing them in the...
  35. DreamWeaver

    MHB A conjecture on a Generalized Barnes' function - can anyone help?

    This is NOT a tutorial, so any and all contributions are very much welcome... :DI've recently been working on the Barnes' function - see tutorial in Math Notes board - and been trying to generalize some of my results to higher order Barnes' functions (intimately connected with the Multiple Gamma...
  36. alyafey22

    MHB A generalized log sine integral .

    This thread will be dedicated to find a general formula for the integral I(a,t) = \int^t_0 x \log|\sin(a x )| \, dx \,\,\,\,\, a,t>0 This is not a tutorial . Any comments or attempts are always be welcomed .
  37. T

    A simple equality of Generalized Lorentz Operators

    Homework Statement Hi we have Lorentz operators J^{\mu\nu} = i(x^{\mu}\partial^{\nu} - x^{\nu}\partial^{\mu}) and these have [J^{\mu\nu}, J^{\rho\sigma}] = i(\eta^{\nu\rho}J^{\mu\sigma} + \eta^{\mu\sigma}J^{\nu\rho} - \eta^{\mu\rho}J^{\nu\sigma} - \eta^{\nu\sigma}J^{\mu\rho}) Now define...
  38. D

    Generalized eigenvectors and differential equations

    Let A be an 3x3 matrix such that A\mathbf{v_1}=\mathbf{v_1}+\mathbf{v_2}, A\mathbf{v_2}=\mathbf{v_2}+\mathbf{v_3}, A\mathbf{v_3}=\mathbf{v_3} where \mathbf{v_3} \neq \mathbb{0}. Let B=S^{-1}AS where S is another 3x3 matrix. (i) Find the general solution of \dot{\mathbf{x}}=B\mathbf{x}. (ii)...
  39. DreamWeaver

    MHB A generalized Arctangent integral/function

    This is NOT a tutorial, so by all means, if you've a mind to, the please DO very much feel free to contribute...Preamble:As a consequence of various families of definite integrals I've been studying recently, I've been led to consider what I've come to call the q-shifted Inverse Tangent Integral...
  40. DreamWeaver

    MHB A generalized Clausen Function, and associated loggamma integrals

    I've recently been working on a number of integrals related to the loggamma function, so I thought I'd share my results here. I'll have to post as and when I have time, and there will be a fair bit of preliminary work before we get to the final results, but - loosely speaking - the main aim here...
  41. alyafey22

    MHB Exploring the Generalized Beta Function: Integrals and Partial Derivatives

    In this thread we consider the integrals of the form \beta(a,b,c;s) = \int^1_0 \frac{1}{(1-x)^a(s-x)^b x^c}\, dx \,\,\,\,\,\,-1<a,b,c<1 \,\,\,s\geq 0 This is NOT a tutorial , all suggestions are encouraged.
  42. D

    Generalized Green function of harmonic oscillator

    Homework Statement The generalized Green function is $$ G_g(x, x') = \sum_{n\neq m}\frac{u_n(x)u_n(x')}{k_m^2 - k_n^2}. $$ Show G_g satisfies the equation $$ (\mathcal{L} + k_m^2)G_g(x, x') = \delta(x - x') - u_m(x)u_m(x') $$ where \delta(x - x') = \frac{2}{\ell}\sum_{n =...
  43. D

    MHB What is Wrong with the Generalized Green Function Equation?

    The generalized Green function is \[ G_g(x, x') = \sum_{n\neq m}\frac{u_n(x)u_n(x')}{k_m^2 - k_n^2}. \] Show \(G_g\) satisfies the equation \[...
  44. B

    Lagrange's Equation Generalized Coordinates

    Hello, I am currently reading about the topic alluded to in the topic of this thread. In Taylor's Classical Mechanics, the author appears to be making a requirement about any arbitrary coordinate system you employ in solving some particular problem. He says, "Instead of the Cartesian...
  45. C

    Generalized Gauss-Codazzi equations

    I've read an article in which a more general version of gauss-codazzi equations are presented namely a version where one has a connection $$\nabla_X Y = '\nabla_X Y + B(X,Y)u$$ where ##'\nabla## is the projection of (the symmetric and metric compatible connection)##\nabla## orthogonal to...
  46. Z

    Euler-Lagrange equation on Lagrangian in generalized coordinates

    Homework Statement I need some help understanding a derivation in a textbook. It involves the Lagrangian in generalized coordinates. Homework Equations The text states that generalized coordinates {q_1, ..., q_3N} are related to original Cartesian coordinates q_\alpha = f_\alpha(\mathbf r_1...
  47. D

    Generalized uncertainty principle

    Homework Statement A spin-half particle is in a known eigenstate of Sz. Show that the product <S^2_x> < S^2_y> is consistent with the Uncertainty principle Homework Equations The Attempt at a Solution I know that the generalized uncertainty principle gives ΔS_x ΔS_y ≥ |<[S_x...
  48. E

    What is the probability of a group of 800 people sharing a specific birthday?

    There is a lot of information on the web about how to calculate the probability that, in an arbitrarily-sized group, 2 people will share a birthday. However, I am trying to determine the probability that a larger number of people are born on a specific day (e.g., a group of people have a...
  49. maverick280857

    Basic question about the generalized Poisson Equation

    Hi, Suppose we look at two dimensional Poisson's equation in a medium with spatially varying (but real) dielectric constant: \nabla(\epsilon_r\nabla \varphi) = -\frac{\rho(x,y)}{\epsilon_0} Consider the problem of solving this using the Finite Difference method on a rectangular grid...
  50. R

    Prediction interval for generalized linear model

    I am currently working on a prediction problem using generalized linear model, My goal is to get the prediction distribution of the response variable. I read a thread (https://stat.ethz.ch/pipermail/r-help/2003-May/033165.html) saying the prediction uncertainty of a generalized linear model...
Back
Top