What is Partial differential equations: Definition and 148 Discussions

In mathematics, a partial differential equation (PDE) is an equation which imposes relations between the various partial derivatives of a multivariable function.
The function is often thought of as an "unknown" to be solved for, similarly to how x is thought of as an unknown number, to be solved for, in an algebraic equation like x2 − 3x + 2 = 0. However, it is usually impossible to write down explicit formulas for solutions of partial differential equations. There is, correspondingly, a vast amount of modern mathematical and scientific research on methods to numerically approximate solutions of certain partial differential equations using computers. Partial differential equations also occupy a large sector of pure mathematical research, in which the usual questions are, broadly speaking, on the identification of general qualitative features of solutions of various partial differential equations. Among the many open questions are the existence and smoothness of solutions to the Navier–Stokes equations, named as one of the Millennium Prize Problems in 2000.
Partial differential equations are ubiquitous in mathematically-oriented scientific fields, such as physics and engineering. For instance, they are foundational in the modern scientific understanding of sound, heat, diffusion, electrostatics, electrodynamics, fluid dynamics, elasticity, general relativity, and quantum mechanics. They also arise from many purely mathematical considerations, such as differential geometry and the calculus of variations; among other notable applications, they are the fundamental tool in the proof of the Poincaré conjecture from geometric topology.
Partly due to this variety of sources, there is a wide spectrum of different types of partial differential equations, and methods have been developed for dealing with many of the individual equations which arise. As such, it is usually acknowledged that there is no "general theory" of partial differential equations, with specialist knowledge being somewhat divided between several essentially distinct subfields.Ordinary differential equations form a subclass of partial differential equations, corresponding to functions of a single variable. Stochastic partial differential equations and nonlocal equations are, as of 2020, particularly widely studied extensions of the "PDE" notion. More classical topics, on which there is still much active research, include elliptic and parabolic partial differential equations, fluid mechanics, Boltzmann equations, and dispersive partial differential equations.

View More On Wikipedia.org
Recent contents Top users
  1. P

    Show uniqueness in Dirichlet problem in unit disk

    Consider the solution of the Dirichlet problem in the unit disk, i.e. solving Laplace equation there with some known function on the boundary. The solution, obtained via separation of variables, can be expressed as $$u(r,\theta)=\frac{a_0}{2}+\sum_{n=1}^\infty...
  2. P

    I On vibrating string and differentiating infinite sum

    Consider a homogeneous vibrating string of length ##\pi## fixed at both endpoints. The deviation from equilibrium is denoted ##u(x,t)## and the vibrations are assumed to be small so that they are at right angle to the ##x##-axis; gravitation is disregarded. The problem can be formulated as...
  3. P

    Solving modified heat equation

    In my Fourier analysis book, the author introduces some basic PDE problems and how one can solve these using Fourier series. I know how to solve basic heat equation problems, but the above one is different from the previous problems I've worked in terms of the boundary conditions. Using...
  4. Safinaz

    Solving Klein Gordon’s equation

    My solution: Let ## \phi (x, t) = F(x) A(t) ##, then Eq. (1) becomes ## \frac{1}{A(t)} \frac{\partial^2}{\partial t^2} - \frac{1}{F(x)} \frac{\partial^2}{\partial x^2} = 0 ## So that : ## \frac{\partial^2}{\partial t^2} = k^2 ~A (t)##, and ## \frac{\partial^2}{\partial x^2} = k^2 ~F...
  5. Safinaz

    How to determine the integration constants in solving the Klein Gordon equation?

    I solved by ## \int d \dot{\phi} = \int d x \to \dot{\phi} = x+ c_1 \to \int d \phi = \int d t ( x+c_1) \to \phi = x t + c_1 t + c_2 ## Is this way correct? To determine ##c_2## use initial condition: ##\phi(0,x)=0## that yields ##c_2=0##, but how to get ##c_1## ?
  6. Philip551

    Looking for resources to help me understand the basics of PDEs for physics

    TL;DR Summary: I am taking a math methods course this semester of which a large part are PDEs. I don't understand the context behind the order in which we are solving PDEs. I am interested in learning how other people were taught PDEs and any book recommendations you might have. I am taking a...
  7. user123abc

    Model CO2 diffusing across the wall of a cylindrical alveolar blood vessel

    TL;DR Summary: Solve heat equation in a disc using fourier transforms Carbon dioxide dissolves in the blood plasma but is not absorbed by red blood cells. As the blood returns to an alveolus, assume that it is well-mixed so that the concentration of dissolved CO2 is uniform across a...
  8. Vanilla Gorilla

    B Incorporating boundary conditions in the Finite Element Method (FEM)

    I have been watching Mike Foster's video series of the Finite Element Method for Differential Equations (FEM). In this episode, he solves a DE relating to temperature. As the final step, he gives the following equation: $$[K] [T] = [F]$$ In this equation, I understand that ##[K]## is the...
  9. T

    A Integrability of Systems of Differential Equations

    I' m reading wiki article about Solitons and have some some troubles to understand the meaning of the following: Question: In context of systems of differential equations, what means precisely "integrability of the equations"? Is there any good intuition how to think about it? Has it some...
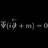
  10. qft-El

    A Solving renormalization group equation in QFT

    I'm learning about the RG equation and Callan-Symanzik equation. In ref.1 they claim to solve the RG equation via the method of characteristics for PDE. Here's a picture of the relevant part: First, the part I don't understand - the one underlined in red. What does "compatible" mean here...
  11. jackkk_gatz

    Heat equation with non homogeneous BCs

    I did a change of variable $$\theta(r,z) = T(r,z)-T_{\infty}$$ which resulted in $$\frac{1}{r}\frac{\partial }{\partial r}(r\frac{\partial \theta}{\partial r})+\frac{\partial^2 \theta}{\partial z^2}=0$$ $$\left.-k\frac{\partial \theta}{\partial r}\right\rvert_{r=R}=h\theta$$...
  12. BloonAinte

    I Finding the time for the first shock for a quasilinear first order PDE

    To find a shock wave, do we always solve the equation ##x_{\xi}=0##? The PDEs I consider are of the form ##u_t + g(u) u_x = f(u)##, with initial condition ##u(x,0) = h(x)##. I have been looking at the solutions for problems in my homework sheet but this method was used with no explanation. Why...
  13. BloonAinte

    I Characteristic curves for ##u_t + (1-2u)u_x = -1/4, u(x,0) = f(x)##

    I woud like to find the characteristic curves for ##u_t + (1-2u)u_x = -1/4, u(x,0) = f(x)## where ##f(x) = \begin{cases} \frac{1}{4} & x > 0 \\ \frac{3}{4} & x < 0 \end{cases}##. By using the method of chacteristics, I obtain the Charpit-Lagrange system of ODEs: ##dt/ds = 1##, ##dx/ds = 1 -...
  14. N

    Correct Usage of Partial Derivative Symbols in PDEs

    Some may say that ##\frac{ \partial g }{ \partial t }## is correct because it is a term in a partial differential equation, but since ##g## is a one variable function with ##t## only, I think ##\frac{ dg }{ dt }## is correct according to the original usage of the derivative and partial...
  15. Magnetons

    PDE and the separation of variables

    using the equation ##u(x,y)=f(x)g(y)##, first, I substitute the value of ##u_{xx}## and ##u_{yy}## in the given PDE. after that solve the ODEs but I can't understand about the ##u_{t}##.In my solution, I put ##u_{t}=0## because u is only the function of x and y. Is it the right approach, to me...
  16. jones1234

    A How can I interpret the 2D advection equation?

    I want to model the advection of debris rock layer with a thickness hd on top of a glacier through ice flow with velocity components u and v. Can anybody explain the physical difference between these 2 equations and which one I should take? Thanks
  17. chwala

    Proof involving ##ω(ξ,n)=u(x,y)## - Partial differential equations

    I am going through this page again...just out of curiosity, how did they arrive at the given transforms?, ...i think i get it...very confusing... in general, ##U_{xx} = ξ_{xx} =ξ_{x}ξ_{x}= ξ^2_{x}## . Also we may have ##U_{xy} =ξ_{xy} =ξ_{x}ξ_{y}.## the other transforms follow in a similar manner.
  18. chwala

    Using separation of variables in solving partial differential equations

    I am reading on this part; and i realize that i get confused with the 'lettering' used... i will use my own approach because in that way i am able to work on the pde's at ease and most importantly i understand the concept on separation of variables and therefore would not want to keep on second...
  19. C

    A Compactness and complexity in electrodynamics

    As human beings, we tend to act and observe and think over time periods spanning a few milliseconds to several decades (or even centuries.) Essentially all phenomena that we directly engage with in everyday life are electrodynamical (with quantum electrodynamics over reasonably short time and...
  20. L

    Is the Fourier Transform Correctly Applied in Solving This Laplace Equation?

    I have tried to Fourier transform in ##x## and get the result in the transformed coordinates, please check my result: $$ \tilde{u}(k, y) = \frac{1-e^{-ik}}{ik}e^{-ky} $$ However, I'm having some problems with the inverse transform: $$ \frac{1}{2\pi}\int_{-\infty}^\infty...
  21. L

    I General solution of heat equation?

    We know $$ K(x,t) = \frac{1}{\sqrt{4\pi t}}\exp(-\frac{x^2}{4t}) $$ is a solution to the heat equation: $$ \frac{\partial u}{\partial t} = \frac{\partial^2 u}{\partial x^2} $$ I would like to ask how to prove: $$ u(x,t) = \int_{-\infty}^{\infty} K(x-y,t)f(y)dy $$ is also the solution to...
  22. Safinaz

    I How to solve this second order differential equation

    Any idea how to solve this equation: ## \ddot \sigma - p e^\sigma - q e^{2\sigma} =0 ## Or ## \frac{d^2 \sigma}{dt^2} - p e^\sigma - q e^{2\sigma} =0 ## Where p and q are constants.Thanks.
  23. P

    Heat Diffusion Equation - Using BCs to model as an orthonormal system

    I've tried to show b) by using the sine Fourier series on ##[0,2a]##, to get ##g_k = \Sigma_{n=0}^{2a} \sqrt\frac{2}{a} Sin(q_k x)## Therefore ##\sqrt\frac{2}{a} = \frac{1}{a} \int_0^{2a} Sin(q_kx)g_k dx## These are equal therefore it is an orthonomal basis. I'm not sure if this is correct so...
  24. S

    Heat Equation with Periodic Boundary Conditions

    I'm solving the heat equation on a ring of radius ##R##. The ring is parameterised by ##s##, the arc-length from the 3 o'clock position. Using separation of variables I have found the general solution to be: $$U(s,t) = S(s)T(t) = (A\cos(\lambda s)+B\sin(\lambda s))*\exp(-\lambda^2 kt)$$...
  25. currently

    Partial Derivative of a formula based on the height of a cylinder

    The function should use (r,z,t) variables The domain is (0,H) Since U is not dependent on angle, then theta can be ignored in the expression for Laplacian in cylindrical coordinates(?)
  26. A

    Partial Differential Equations result -- How to simplify trig series?

    Solve the boundary value problem Given u_{t}=u_{xx} u(0, t) = u(\pi ,t)=0 u(x, 0) = f(x) f(x)=\left\{\begin{matrix} x; 0 < x < \frac{\pi}{2}\\ \pi-x; \frac{\pi}{2} < x < \pi \end{matrix}\right. L is π - 0=π λ = α2 since 0 and -α lead to trivial solutions Let u = XT X{T}'={X}''T...
  27. E

    A How to get a converging solution for a second order PDE?

    I have been struggling with a problem for a long time. I need to solve the second order partial differential equation $$\frac{1}{G_{zx}}\frac{\partial ^2\phi (x,y)}{\partial^2 y}+\frac{1}{G_{zy}}\frac{\partial ^2\phi (x,y)}{\partial^2 x}=-2 \theta$$ where ##G_{zy}##, ##G_{zx}##, ##\theta##...
  28. Safder Aree

    How to apply the Fourier transform to this problem?

    I am struggling to figure out how to approach this problem. I've only solved a homogenous heat equation $$u_t = u_{xx}$$ using a Fourier transform, where I can take the Fourier transform of both sides then solve the general solution in Fourier terms then inverse transform. However, since this...
  29. F

    I Separation of Variables for Partial Differential Equations

    When using the separation of variable for partial differential equations, we assume the solution takes the form u(x,t) = v(x)*g(t). What is the justification for this?
  30. T

    A Determine PDE Boundary Condition via Analytical solution

    I am trying to determine an outer boundary condition for the following PDE at ##r=r_m##: $$ \frac{\sigma_I}{r} \frac{\partial}{\partial r} \left(r \frac{\partial z(r,t)}{\partial r} \right)=\rho_D gz(r,t)-p(r,t)-4 \mu_T \frac{\partial^2z(r,t)}{\partial r^2} \frac{\partial z(r,t)}{\partial t} $$...
  31. M

    A Laplace or Fourier Transform to solve a system of partial differential equations in thermoelasticity

    I've a system of partial diff. eqs. in thermo-elasticity, I can solve it using normal mode analysis method but I need to solve it using laplace or Fourier
  32. H

    Partial Differential Equation Mathematical Modelling

    Salutations, I have been trying to approach a modelling case about organism propagation which reproducing with velocity $$\alpha$$ spreading randomly according these equations: $$\frac{du(x,t)}{dt}=k\frac{d^2u}{dx^2} +\alpha u(x,t)\\\ \\ u(x,0)=\delta(x)\\\ \lim\limits_{x \to \pm\infty}...
  33. Rupul Chandna

    I Why is separation constant l(l+1) instead of +-l^2?

    While separating variables in the Schrodinger Equation for hydrogen atom, why are we taking separation constant to be l(l+1) instead of just l^2 or -l^2, is it just to make the angular equation in the form of Associated Legendre Equation or is there a deeper meaning to it?
  34. A

    MHB Partial differential equations problem - finding the general solution

    4\frac{\partial u}{\partial t}+\frac{\partial u}{\partial x} = 3u , u(x,0)=4e^{-x}-e^{-5x} let U =X(x)T(t) so 4X\frac{\partial T}{\partial t}+T\frac{\partial X}{\partial x} = 3XT 4\frac{\partial T}{T \partial t}+\frac{\partial X}{X \partial x} = 3 \left( 4\frac{\partial T}{T...
  35. M

    MATLAB Solving Chromatography PDE with MOL and ode15s

    Hello all I am using the method of lines to solve the following PDE: ## \frac {\partial C} {\partial t} + F\frac {\partial q} {\partial t} + u \frac {dC} {dz} = D_{ax} \frac{\partial^2 C} {\partial z^2} ## ## \frac {\partial q} {\partial t} = k (q^{*}-q) ## With these initial conditions: ##...
  36. G

    Calculus Ordinary and partial differential equations

    Hi, I'm attempting to learn differential equations on my own. Does anyone recommended a textbook that comes with/has a solution manual? I learn faster when I can see a problem worked out if I can't solve it. Thanks.
  37. Peter Alexander

    Solving Second Order Partial Derivative By Changing Variable

    1. The problem statement, all variables, and given/known data Given is a second order partial differential equation $$u_{xx} + 2u_{xy} + u_{yy}=0$$ which should be solved with change of variables, namely ##t = x## and ##z = x-y##. Homework Equations Chain rule $$\frac{dz}{dx} = \frac{dz}{dy}...
  38. Peter Alexander

    Solving Partial Differential Equation

    1. The problem statement, all variables, and given/known data Task requires you to solve a partial differential equation $$u_{xy}=2yu_x$$ for ##u(x,y)##. A hint is given that a partial differential equation can be solved in terms of ordinary differential equations. According to the solution...
  39. A

    A How to simplify the solution of the following linear homogeneous ODE?

    During solution of a PDE I came across following ODE ## \frac{d \bar h}{dt} + \frac{K}{S_s} \alpha^2 \bar h = -\frac{K}{S_s} \alpha H h_b(t) ## I have to solve this ODE which I have done using integrating factor using following steps taking integrating factor I=\exp^{\int \frac{1}{D} \alpha^2...
  40. B

    A Difficult partial differential Problem

    Problem: $${\frac {\partial }{\partial t}}A\left( y,t \right) +6\,\Lambda\,\Omega\, \left( {y}^{2}-y \right) \sin \left( t \right) ={\frac {\partial ^{2}}{\partial {y}^{2}}}A \left( y,t \right)$$ $${\frac{\partial }{\partial y}}A \left( t,0 \right) ={\frac {\partial }{\partial y}}A \left( t,1...
  41. J6204

    Calculating the Fourier integral representation of f(x)

    Homework Statement Considering the function $$f(x) = e^{-x}, x>0$$ and $$f(-x) = f(x)$$. I am trying to find the Fourier integral representation of f(x). Homework Equations $$f(x) = \int_0^\infty \left( A(\alpha)\cos\alpha x +B(\alpha) \sin\alpha x\right) d\alpha$$ $$A(\alpha) =...
  42. J6204

    Extending function to determine Fourier series

    In the following question I need to find the Fourier cosine series of the triangular wave formed by extending the function f(x) as a periodic function of period 2 $$f(x) = \begin{cases} 1+x,& -1\leq x \leq 0\\ 1-x, & 0\leq x \leq 1\\\end{cases}$$ I just have a few questions then I will be able...
  43. S

    A How to find the partial derivatives of a composite function

    Hello, dear colleague. Now I'm dealing with issues of modeling processes of heat and mass transfer in frozen and thawed soils. I am solving this problems numerically using the finite volume method (do not confuse this method with the finite element method). I found your article: "Numerical...
  44. grquanti

    I Substitution in partial differential equation

    Hello everybody. Consider $$\frac{\partial}{\partial t}f(x) + ax\frac{\partial }{\partial x}f(x) = b x^2\frac{\partial^2}{\partial x^2}f(x)$$ This is the equation (19) of...
  45. K

    A A system of partial differential equations with complex vari

    Hi, I need to solve a system of first order partial differential equations with complex variables given by What software should I use for solving this problem..? The system includes 13 differential equations ...
  46. awholenumber

    I What are partial differential equations?

    If the slope of the curve (derivative) at a given point is a number .
  47. R

    A Converting Partial Differential Equations to Frequency Domain

    Hello All, I would like to convert a partial diff equation in time domain into frequency domain, however there is a term of the form: Re(∇(E1.E2*) exp(j[ω][/0]t)) where E1 and E2 are the magnitudes of the electric field and [ω][/0] is the angular frequency. Can someone please help me to...
  48. FranciscoSili

    I Help Solving an Equation with a Boundary Condition

    Hello everybody. I'm about to take a final exam and I've just encountered with this exercise. I know it's simple, but i tried solving it by Separation of variables, but i couldn't reach the result Mathematica gave me. This is the equation: ∂u/∂x = ∂u/∂t Plus i have a condition...
  49. Conservation

    What is the inverse Fourier transform of e^3iωt for solving ut+3ux=0?

    Homework Statement Solve ut+3ux=0, where -infinity < x < infinity, t>0, and u(x,0)=f(x).Homework Equations Fourier Transform where (U=fourier transform of u) Convolution Theorem The Attempt at a Solution I've used Fourier transform to get that Ut-3iwU=0 and that U=F(w)e3iwt. However, I'm...
  50. K

    Courses Maths for Experimental Physics?

    Hi all, I'm currently a second year Applied Maths and Physics student. I will be specialising in Experimental physics next year. With this, I will have no more core (mandatory) mathematics modules. So far, I have taken, Linear Algebra I, Calculus, Differential Equations, Linear Algebra II...
Back
Top