Rotating Definition and 1000 Threads
-

MHB Volume of the solid obtained by rotating R around the line y=x
Let $R$ be the region $\left\{(x, y) : 0 \leq x \leq 1, 3^x − x − 1 \leq y \leq x\right\}$. Find the volume of the solid obtained by rotating $R$ around the line $y = x$. -
A
Undergrad Relativistic Energy of Rotating Thin Ring: Quick Qs
Quick question about the relativistic energy of a rotating thin ring, hoop or cylinder. Is there any reason why the relativistic energy would be anything different than ##E=\gamma_t m_0 c^2## where ##\gamma_t## depends on the tangential velocity ##v_t## observed by someone at rest with the...- AVentura
- Thread
- Angular momemtum Energy Relativistic Relativistic energy Relativitiy Ring Rotating
- Replies: 13
- Forum: Special and General Relativity
-

Rotating Pendulum: Is This Eqn Correct?
is this eqn correct- Prabs3257
- Thread
- Moment of inertia Pendulum Rotating Rotational dynamics
- Replies: 2
- Forum: Introductory Physics Homework Help
-

High School What is the angular velocity in the center of a rotating disc?
I have a disc. The center of the disc is its center of mass and the motion of the disc is purely rotational (no translation). What is the angular velocity in the center of the rotating disc?- Seth Greenberg
- Thread
- Angular Angular velocity Center Disc Rotating Rotating disc Velocity
- Replies: 6
- Forum: Mechanics
-

EMF induced in a rotating rod having mass
I first calculated induced emf and then calculated torque about O.But what will i do further.I think i need to find current and then fidn emf=IR. Help please.- Physics lover
- Thread
- Emf Induced Induced emf Mass Rod Rotating
- Replies: 6
- Forum: Introductory Physics Homework Help
-

Probability of hitting a rotating disc
There are two points of the smaller disck such that a line is tangent to the two discks and passes by that point. If the particle leaves of any point belongin to the arch that connects these two points, then it will hit the other disck. So I managed to calculate the value of this arch and divide...- Moara
- Thread
- Disc Probability Rotating Rotating disc
- Replies: 9
- Forum: Introductory Physics Homework Help
-

Why is my answer for the rotating wedge problem not matching?
I tried making the fbd of both blocks the block on the incline will have mgsin30 friction force, tension and centrepetal force's cos component similarly second block will have mg tension and friction where normal will be centrepetal force after solving my ans is not matching- Prabs3257
- Thread
- Laws of motion Rotating Wedge
- Replies: 7
- Forum: Introductory Physics Homework Help
-
S
High School What happens to speed and velocity in a rotating frame of reference?
Let's say I can see a star in a distance of 1ly in front of me. I'm sitting on an office chair and begin to rotate with a speed of 1/s (1 rotation per second). Then I consider me as not rotating and everything else as rotating. Now I will see the star traveling a circular path with the...- somega
- Thread
- Frame Rotating Rotating frame Speed
- Replies: 29
- Forum: Special and General Relativity
-

Rotating an ellipse to create a spheroid?
I was able to find the equation of an ellipse where its major axis is shifted and rotated off of the x,y, or z axis. However, I could not find anywhere an equation for a spheroid that does not have its axis or revolution along the x,y, or z axis. How might I go about deriving such an...- gary0000
- Thread
- Calculus Ellipse Ellipsoid Geometry Rotating
- Replies: 2
- Forum: Calculus and Beyond Homework Help
-

Graduate Advantages of Polar Coordinate System & Rotating Unit Vectors
What is the advantage of using a polar coordinate system with rotating unit vectors? Kleppner's and Kolenkow's An Introduction to Mechanics states that base vectors ##\mathbf{ \hat{r}}## and ##\mathbf{\hat{\theta}}## have a variable direction, such that for a Cartesian coordinates system's base...- torito_verdejo
- Thread
- Coordinate Coordinate system Polar Rotating System Unit Unit vectors Vectors
- Replies: 7
- Forum: Optics
-
K
Plotting a rotating ellipse trajectory (the Moon orbiting the Earth in 2D)
I'm tasked with drawing the trajectory of the Moon around the Earth (in 2D), taking into account the fact that the trajectory also undergoes precession, so the elliptical orbit rotates about it's center (I think it should rotate around the Earth-Moon barycenter, but for the first step I...- kiloNewton
- Thread
- 2d Earth Ellipse Moon Plotting Rotating Rotations Trajectory
- Replies: 2
- Forum: Engineering and Comp Sci Homework Help
-

Graduate How to Zip Through a Rotating Tunnel Without Bumping Into the Walls
[url="https://www.physicsforums.com/insights/how-to-zip-through-a-rotating-tunnel-without-bumping-into-the-walls/"]Continue reading... -
A
Maintain a constant velocity for a rotating wheel
I want to make a small mechanical calculator with no electric parts, nothing too advanced but a few binary gates capable of some basic functions. All the examples I were able to find were amazing but were still dependent on electricity to drive the mechanism. One possibility is a spring but I...- AamsterC2
- Thread
- Constant Constant velocity Mechanical design Rotating Velocity Wheel
- Replies: 4
- Forum: Mechanical Engineering
-
N
Lenz's Law for a rotating PM motor rotor spinning in a thin CU tube
The motor is required to operate at its resonance frequency and I am looking to add a thin-walled (0.010") copper tube inside the stator bore to add some damping. The current motor air-gap is 0.015". If I install a copper tube in the stator bore bonded to the stator and leave a 0.005" air-gap...- Neumahn
- Thread
- Damping Law Lenz's law Magnetics Motor Motors Rotating Rotor Spinning Tube
- Replies: 4
- Forum: Electrical Engineering
-

Undergrad Is it possible to have synchronized clocks in a rotating system?
Consider a wagon with length L and constant speed v on the straight part of a rail. The wagon has clocks on both ends that are sync in the co-moving frame (of the wagon and the clocks). Then there is a curve in the rail with radius r. The speed of the wagon in the curve is still constant v, but...- Foppe Hoekstra
- Thread
- Clocks Rotating System
- Replies: 55
- Forum: Special and General Relativity
-
N
Rotating with slipping to rotating without slipping?
It seems to me that this transition implies going from kinetic friction to static friction. The kinetic friction would apply a torque that would slow down the object's angular velocity, but I'm not sure how this connects to the object suddenly transitioning into rotating without slipping.- nomnom123
- Thread
- Angular acceleration Angular velocity Friction Friction and inertia Rotating Rotation Slipping
- Replies: 3
- Forum: Introductory Physics Homework Help
-
S
Impact force calculation due to a rotating object in Overspeed Trip Valve Design
Bolt comes out by distance d=1.58 mm when speed of rotation of shaft reaches its trip value (w_trip). m is mass of trip weight (Bolt assembly) One of the approach which I had considered is work energy theorem. Initial energy = 0.5m*(w_trip*(r+d))^2 Final Energy= 0.5m*(w_trip*r)^2 (Assuming bolt...- SurajS
- Thread
- Calculation Design Force Impact Impact force Rotating Valve
- Replies: 11
- Forum: Mechanical Engineering
-
S
Graduate Rotating Sphere: Conceptual Question
As shown in figure there's a homogeneous solid sphere. It is rotating about axis which is passing through point P directed perpendicular to the plane of paper. (In short like a pendulum). I'm neglecting gravity and assuming a force F which is directed perpendicular to the string. (The string... -

Undergrad Rotation or acceleration defined without relation to something else
Starting from this post, we are able to define the concept of (proper) acceleration or rotation without any reference to something else About this definition which is the physical meaning of gyroscopes axes pointing in three mutually orthogonal spacelike directions ? In other words, from a...- cianfa72
- Thread
- Acceleration Gyroscopes Relation Rotating Rotation Special relativity
- Replies: 24
- Forum: Special and General Relativity
-
M
High School Polarized Electron in a Rotating Reference Frame
I tried asking a similar question in cosmology but got no answer there so here goes... Suppose I am on a windowless spacecraft in the middle of an intergalactic void. I know that the spacecraft is spinning from measuring the centrifugal forces but have no way of observing the outside...- metastable
- Thread
- Electron Frame Reference Reference frame Rotating
- Replies: 37
- Forum: Special and General Relativity
-
R
Graduate Does thrust get cancelled by a rotating crank?
I have a frame which supports a crank rotating through 360°. The crank lifts a 30 kg weight 540 times a minute ( 540 rpm). As the crank moves 0° to 90° the weight is accelerated to full speed which means it has thrust but then from 90° to 180° it is slowed to a stop then from 180° to 270° it is... -

Rotating Disk and Hanging Mass Calcululations
I used the above equations to solve for tension, torque, inertia, and angular acceleration. Are the formulas I used correct for the given system? How can I calculate Inertia from the trendline equation, I'm drawing a blank.- badger1999
- Thread
- Angular acceleration Disk Inertia Mass Rotating Rotating disk Tension Torque and rotation
- Replies: 1
- Forum: Introductory Physics Homework Help
-
J
Graduate Describing a Rotating Vector with Changing Angular-Velocity
I have a question about a rotating vector field: if there is a vector ##A^i(t_0)## at the origin in coordinate space ##IR^3## , when ##t≥t_0##, the vector rotates with a changing angular-velocity ##ω^i(t)##. then we can get a rotating vector field ##A^i(t)##. then how to describe ##A^i(t)##...- Jianbing_Shao
- Thread
- Rotating Vector
- Replies: 4
- Forum: Special and General Relativity
-

Graduate Ideas for determining the volume of a rotating object
Hello everybody, I am currently working on an experiment investigating the formation of planets. I have a vacuum chamber in which dust particles form bigger agglomerates through accretion (sticking together). From the imagery I can see those agglomerates which are build up by smaller...- Lardos
- Thread
- Ideas Integration Rotating Rotation Volume
- Replies: 7
- Forum: Astronomy and Astrophysics
-
?
Graduate Rotating sphere which separates into hemispheres
Hi all, The scenario I'm considering is a solid sphere (of uniform density) rotating with constant angular velocity when it abruptly splits into two hemispheres along a cut which contains the rotation axis. The hemispheres will begin to separate; if, for example, we consider the rotation to be... -
M
Calculate the radius of this rotating wheel
Homework Statement Calculate radius of rotating wheel. Linear speed of point "a" (red dot) is 2.5 times faster than linear speed of point "b"(blue dot) that is 5cm closer to center of wheel. Right answer is 8.33cm. I drew a sketch without linear line. Homework EquationsThe Attempt at a...- MisterP
- Thread
- Radius Rotating Wheel
- Replies: 9
- Forum: Introductory Physics Homework Help
-

Undergrad Flow (liquid or gas) across a rotating surface's face
<< Mentor Note -- Two threads on the same question merged into one thread >> How does the maximum Power equation change if there's an angle to the way the wind falls into the wind turbine's blades? Example, when it falls vertically to the blades, it's Pmax= 8/27Sρu13 But if there's for...- QuarkDecay
- Thread
- Angle Flow Gas Law Liquid Rotating Surface Turbine Wind
- Replies: 5
- Forum: Mechanics
-
L
Undergrad Can Rotating Magnets Create a Stronger Magnetic Field?
hello, i have a doubt i bought some small neodimium magnets 8x3mm and now i would like to try some experiments with them i have a doubt: if i rotate one of these magnet around one of its parallel axis, very fast , near 1000000 rpm, what happens to the magnetic field produced by the magnet? if...- lovicodo
- Thread
- Fields Magnetic Magnetic fields Rotating
- Replies: 5
- Forum: Electromagnetism
-

Problem 9.2 Classical Mechanics: Astronaut in a rotating space station
Homework Statement Acceleration experienced by an astronaut in a rotating space station. Homework Equations What force would he experience is his own rotating frame of reference. The Attempt at a Solution Newton's second Law for a rotating frame is: mr'' = F net+ Fcor + Fcf Fnet (In the...- SebastianRM
- Thread
- Astronaut Classical Classical mechanics Mechanics Newton 2nd law Physics Rotating Rotational acceleration Space Space station
- Replies: 1
- Forum: Introductory Physics Homework Help
-

Solving Rotating Ice Skaters Problem: Is their Straight Line Parallel?
Statement of the problem : Two ice skaters circle about a point while holding hands. At a certain moment both let go and move along straight lines. Are the two straight lines parallel? Explain. My attempt : Calling the two ice skaters ##S_1## and ##S_2 ##, they must lie...- brotherbobby
- Thread
- Ice Rotating
- Replies: 7
- Forum: Introductory Physics Homework Help
-

Graduate Rotating physicist and momentum conservation
We are aware of the well-known problem of a rotating physicist whose angular velocity ω increases as a consequence of angular momentun conservation (##I_1 \omega_1 = I_2 \omega_2, \Sigma \tau_e = 0##). I am assuming that the net external force (##\Sigma F_e##) is also zero along with the net...- brotherbobby
- Thread
- Conservation Momentum Momentum conservation Physicist Rotating
- Replies: 12
- Forum: Mechanics
-
S
EMF induced in rotating rod inside uniform magnetic field
Homework Statement A 40 cm rod is rotated about its centre inside a region of uniform magnetic field of 6.4 T. Given that the speed of rotation is 15 rad/s, find potential difference between the centre and either end of the rod Homework Equations emf = - ΔΦ / Δt ω = 2π / T The Attempt at a...- songoku
- Thread
- Emf Field Induced Magnetic Magnetic field Rod Rotating Uniform Uniform magnetic field
- Replies: 6
- Forum: Introductory Physics Homework Help
-
T
A ball (sphere) rotating along a moving incline
Homework Statement We have a ball of mass ##m##and radius ##r##. it is placed on an incline (We don't know the angle of the incline, nor we do whether the angle is constant along the incline - maybe it is a curved incline) and then released. The COM of ball is ##h## meters above the incline at...- titansarus
- Thread
- Ball Dynamics Incline Mechanic Rolling ball Rolling friction Rotating Sphere
- Replies: 14
- Forum: Introductory Physics Homework Help
-

Shape of a bubble inside a rotating container
1. A closed cylindrical vessel filled with water (at room temperature) contains a small air bubble of normal pressure and volume ##V=1~{cm}^3## inside in it.The cylinder is then started to be rotated slowly with a small angular acceleration in a complete weightlessness (at a space station)...- Raihan amin
- Thread
- Bubble Container Fluid dynamics Rotating Shape Surface tension Thermodaynamics
- Replies: 5
- Forum: Advanced Physics Homework Help
-

Power generated by a coil rotating in magnetic field
The problem: a coil of radius r, length l and N turns, rotating with constant angular velocity ω around an axis perpendicular to its simmetric axis and passing for the center of the coil. The coils is submersed in a static magnetic field, intensity B0, perpendicular to the axis of rotation of...- marino
- Thread
- Coil Field Magnetic Magnetic field Power Power dissipated Resistor Rotating Solenoid
- Replies: 3
- Forum: Electrical Engineering
-
Conservation of Energy and Angular Momentum in a Rotating Train-Disk System
Homework Statement [/B] A train stands in the middle of a rotating disk with an initial angular velocity of $\omega_i$. The mass of the train is m and the moment of inertia of the train-disk is I. At one point the train departs on a straight track to a distance R from the disk's centre. (R...- JD_PM
- Thread
- Angular momemtum Disk Newtonian mechanics Rotating Rotating disk Train
- Replies: 30
- Forum: Introductory Physics Homework Help
-
E
Slowly Rotating Device For a Camera Pan Timelapse
Hello all! I just discovered PF as I have been searching about a project I have been pondering for a day. The idea is to have a device that I can set my 3lb camera and have the device rotate left-to-right && || right-to-left over the duration of 2 hours for use in a sunset/cloud timelapse...- EzraF
- Thread
- Camera Dc motor Device Gear Rotating Rpm Torque and rotation
- Replies: 12
- Forum: Mechanical Engineering
-
F
Graduate Body rotating about its center of mass
Hello, As many know, when an external force acts on a rigid body and the force's line of action does not pass through the body's center of mass ##c.m.##, the force will cause the body to both translate and rotate exactly about the ##c.m.##. Otherwise, the body will solely translate without... -
F
How to calculate vibrations on a rotating shaft?
Is there a way to calculate the vibrations on a shaft rotating at a certain rpm? Is there a way to accurately simulate this?- friscoboya
- Thread
- Rotating Shaft Vibrations
- Replies: 4
- Forum: Mechanical Engineering
-
L
Graduate Quick Question: Rate of Change of a Rotating Vector
Is the equation presented (that the time-derivative of a given vector in such a scenario is equal to its angular frequency vector cross the vector itself) true in the case of a vector whose origin is not on the axis of rotation? The way I'm visualizing this, if we take such a displaced origin... -

Frictional force between two rotating cylinders
Homework Statement .A cylinder P of radius rP is being rotated at a constant angular velocity ωP along positive y-axis with the help of a motor about its axis that is fixed. Another cylinder Q of radius rQ free to rotate about its axis that is also fixed is touched with and pressed on P making...- Dayal Kumar
- Thread
- Cylinders Force Frictional force Mechanics Rotating Rotational dynamics Rotational kinematics
- Replies: 11
- Forum: Introductory Physics Homework Help
-

Graduate Rotating speed of a proton ion
I tried to calculted the rotating speed fro a proton from the clasical point of view by using its magnetic moment and the moment of a rotating sphere uniformly charged as example here: https://ocw.mit.edu/courses/physics/8-07-electromagnetism-ii-fall-2012/exams/MIT8_07F12_quizsol2.pdf It is said...- Javier Lopez
- Thread
- Ion Magnetic field Magnetic moment Proton Rotating Speed
- Replies: 12
- Forum: Mechanics
-

Deriving Ball Movement on Northern Hemisphere with Rotating Reference Frame
I have a ball of mass m that is situated on horizontal plane on the northern Hampshire. I am asked to show that the ball is moving, clockwise, in a manner of r = v / ( 2Ω*sin(λ) ) where v is the ball's velocity, Ω is Earth's angular velocity, and λ is the terrestrial latitude So here's what...- physicschick21
- Thread
- Advance physics Celestial mechanics Coriolis Frame Reference Reference frame Rotating
- Replies: 8
- Forum: Advanced Physics Homework Help
-
J
Torque of a rotating wheel on a static wheel
Homework Statement A uniform cylindrical wheel of mass ##m_{1}## and radius ##R_{1}## rotates with angular velocity ##\omega_{1}##. It lies a certain distance (along the same axis) from a static wheel of radius ##R_{2}## and mass ##m_{2}##. The wheels are then pushed against each other with a...- Jenny Physics
- Thread
- Newton 2nd law Rotating Rotational mecahnics Static Torque Torque and rotation Wheel
- Replies: 17
- Forum: Calculus and Beyond Homework Help
-
C
Graduate Conservation of Angular Momentum on a rotating disc
I have a disc that is rotating due to air being blown at its outer radius. The incoming relative velocity of the air is high, therefore the effect of friction supersedes the effect of conservation of angular momentum. The tangential portion of this velocity decreases due to the friction as it...- CullenWillett
- Thread
- Angular Angular momentum Conservation Disc Momentum Rotating Rotating disc
- Replies: 22
- Forum: Mechanics
-
S
Undergrad Is Constant Linear Velocity Possible in Rotating Particles?
If talking about a particle rotating around an axis away from it by r. if the particle is moving with constant angular velocity ω. is the linear velocity constant or no? Now what I know is that since we have Vt= ωr, so r doesn't change, as well as ω, so Vt is said to be constant. but I think... -
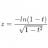
Graduate Artificial gravity in a rotating space station
It is often proposed that gravity could be simulated on a space station by rotating around an axis, such that the astronaut experiences the centripetal force of the space station wall, analogously to gravity. It is usually mentioned that the radius of rotation must be very large to avoid...- substitute materials
- Thread
- Artificial gravity Gravity Rotating Space Space station
- Replies: 28
- Forum: Mechanics
-
N
Undergrad Rotating Coordinates: Solving for x and y
If one rotates a tangent plane on a curved surface, this point can be expressed as follows: x' = x cos(theta) - y sin(theta) y' = x sin(theta) + y cos(theta) One solves for x and y and computes based on the deviation of the deviation. My question is: would the answer differ if you choose a...- Nusc
- Thread
- Coordinates Rotating
- Replies: 4
- Forum: Differential Geometry
-
G
MHB Rotate Point p: How to Rotate by 75° Counterclockwise
My problem reads as follows: Point p=(3,3√3) is rotated counterclockwise about the origin by 75 degrees. What are the coordinates after this rotation? I have no idea how to rotate a point, let alone by 75 degrees.- GloriousGoats
- Thread
- Point Rotating
- Replies: 3
- Forum: General Math
-
D
Calculating the relevant variables for a rotating habitat
1. Homework Statement I want to calculate the rotational period and surface velocity of a Bishop Ring with a radius of 80 km and a surface 'gravity' of 0.86 G I should note that this isn't for homework. It's for personal interest. I'm looking for a sanity check on this. The homework forum...- DET
- Thread
- Rotating Variables
- Replies: 2
- Forum: Introductory Physics Homework Help