mfu
- 5
- 0
Question 1
1. Homework Statement
The drawing shows a snapshot of a transverse wave traveling along a string at 9.6 m/s. The equation for the wave is y(x, t) = A cos(ωt + kx).
At what times could this snapshot have been taken? (Give the three smallest nonnegative possibilities.)
Found the following:
A= 2mm
ω= 1507.96447 rad/s
k= 157.07963 rad/m
time1= 1.04ms
time2= 5.21ms
time3= 9.38ms
The problem I have is that time 1 is incorrect while the other 2 are. To find the times, I used the setup found in this post but with my values:
https://www.physicsforums.com/showpost.php?p=2690152&postcount=6
Not sure what I could be doing wrong. Also, could someone explain where the person got the 2pi, 4pi, and 6pi in the above link? Don't quite understand it.Question 2
1. Homework Statement
The pulse of the figure travels to the right on a string whose ends at x = 0 and x = 12.0 m are both fixed in place. Imagine a reflected pulse that begins to move onto the string at an endpoint at the same time the incident pulse reaches that endpoint. The superposition of the incident and reflected pulses gives the shape of the string. When is the next time t that the string referred to in the figure looks exactly as it does at t = 0? (Answer in seconds.)
Image:
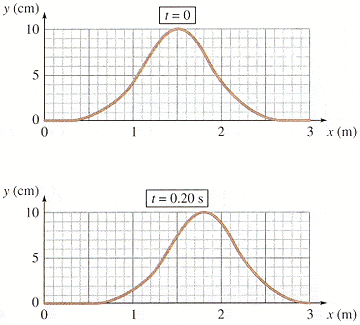
I have no idea what to do for this one. Just plain stumped. Any tips such as what equation(s) to use would be very helpful.
Thanks in advance to anyone that can help me with these 2 problems!
1. Homework Statement
The drawing shows a snapshot of a transverse wave traveling along a string at 9.6 m/s. The equation for the wave is y(x, t) = A cos(ωt + kx).
At what times could this snapshot have been taken? (Give the three smallest nonnegative possibilities.)
The Attempt at a Solution
Found the following:
A= 2mm
ω= 1507.96447 rad/s
k= 157.07963 rad/m
time1= 1.04ms
time2= 5.21ms
time3= 9.38ms
The problem I have is that time 1 is incorrect while the other 2 are. To find the times, I used the setup found in this post but with my values:
https://www.physicsforums.com/showpost.php?p=2690152&postcount=6
Not sure what I could be doing wrong. Also, could someone explain where the person got the 2pi, 4pi, and 6pi in the above link? Don't quite understand it.Question 2
1. Homework Statement
The pulse of the figure travels to the right on a string whose ends at x = 0 and x = 12.0 m are both fixed in place. Imagine a reflected pulse that begins to move onto the string at an endpoint at the same time the incident pulse reaches that endpoint. The superposition of the incident and reflected pulses gives the shape of the string. When is the next time t that the string referred to in the figure looks exactly as it does at t = 0? (Answer in seconds.)
Image:
I have no idea what to do for this one. Just plain stumped. Any tips such as what equation(s) to use would be very helpful.
Thanks in advance to anyone that can help me with these 2 problems!
Last edited by a moderator: