- #1
jackfrost1031
- 4
- 0
Hi,
I think i should have posted here instead of where I posted before. I don't know how I missed the homework help section... anyway
Well, I'm required to solve this heat transfer problem.
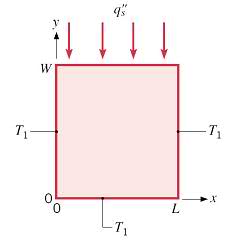
T1 is 25c and q'' is 100w/m2
Ok, so I can get it to do it in 1 dimension and my numbers are correct based upon past work done in Excel (checked by Prof). I am not sure how to combine two dimensions into one matrix.
Currently my code is as follows:
T1 comes out to
T1 =
25.901
15.901
7.8263
5.6215
7.6328
15.369
25
which is precisely what it should be [if this were a 1D problem].
I realize that it's stuck at the current size and I can work on making it capable of whatever size later; right now I want a 5x5 mesh plus the boundaries so, really 7x7.
I have derived equations from an energy balance for all the different types of nodes (corner, interior, boundary, etc) but I'm unsure how to get them to work together in this scheme. I can do it iteratively but it's not what he wants.
Could someone help me out a little here? Do I need to have a 7x7 solution matrix? (ugh, please not!)
I think i should have posted here instead of where I posted before. I don't know how I missed the homework help section... anyway
Well, I'm required to solve this heat transfer problem.
Develop a MATLAB code that computes the two-dimensional
temperature distribution in the rectangular plate. Load coefficients
into a matrix array of the form [A][T] = [C] where [A] is an M by
N matrix containing the leading coefficients of the temperature
nodes derived from the energy balance procedure of Task 1.
Solve the system of equations using MATLAB’s routine [T]= [A ]^-1*[C]
T1 is 25c and q'' is 100w/m2
Ok, so I can get it to do it in 1 dimension and my numbers are correct based upon past work done in Excel (checked by Prof). I am not sure how to combine two dimensions into one matrix.
Currently my code is as follows:
Code:
%{
Zach Cross
7-17-2010
Computes 2D temperature distribution in a rectangular plate
%}
clear all; close all; format short g
%boundaries
T1 = 25;
TE = T1;
TS = T1;
TW = T1;
%degrees C
q = 100;
%w/m^2
L = 0.2;
W = 0.1;
% meter
k = 0.1;
%W/(m*K)
%size of matrix
i = 5;
j = 5;
dx = L/i;
dy = W/j;
%set some helpful constants
dx_ = dx/dy;
dy_ = dy/dx;
d1 = (3*k*dx_ + 3*k*dy_);
d2 = (3*k*dx_ + 2*k*dy_);
d3 = (2*k*dx_ + 3*k*dy_);
d4 = (2*k*dx_ + 2*k*dy_);
%west interior node going from north to south (not accounting for 25c west boundary condition)
A1 = [1, -1, 0, 0, 0, 0, 0;
-2*k*dx_/d1, 1, -k*dx_/d1, 0, 0, 0, 0;
0, -k*dx_/d3, 1, -k*dx_/d3, 0, 0, 0;
0, 0, -k*dx_/d3, 1, -k*dx_/d3, 0, 0;
0, 0, 0, -k*dx_/d3, 1, -k*dx_/d3, 0;
0, 0, 0, 0, -k*dx_/d1, 1, -2*k*dx_/d1;
0, 0, 0, 0, 0, 0, 1];
C1 = [q*dy/(2*k);
0;
0;
0;
0;
0;
TS];
T1 = inv(A1)*C1T1 comes out to
T1 =
25.901
15.901
7.8263
5.6215
7.6328
15.369
25
which is precisely what it should be [if this were a 1D problem].
I realize that it's stuck at the current size and I can work on making it capable of whatever size later; right now I want a 5x5 mesh plus the boundaries so, really 7x7.
I have derived equations from an energy balance for all the different types of nodes (corner, interior, boundary, etc) but I'm unsure how to get them to work together in this scheme. I can do it iteratively but it's not what he wants.
Could someone help me out a little here? Do I need to have a 7x7 solution matrix? (ugh, please not!)