mrshappy0
- 97
- 0
Homework Statement
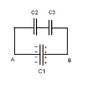
Initially switch is at A, and C1 is fully charged (batter=12volts). C2,C3 are initially uncharged.
Then switch is moved to B and the charge is redistributed.
What is the voltage across C1? [Answer: 8.00volts]
What is the voltage across C3? [Answer: 2.67volts]
Homework Equations
C=Q/V
Series:
1/Ceq=1/C1+1/C2
Q=Q1=Q2
V=V1+V2
The Attempt at a Solution
The question does not state a time after the switch is closed. Does the time not matter or should I assume it means A LONG TIME AFTER?
If it meant a long time after, I assumed that the original voltage of 12 volts is shared and the charge is equivalent for all capacitors. Thus C123=40/3 pF and Q123= C123*Vb=(40/3)*12=160... Then V1=Q123/C1=160/40=4pF but this is incorrect