A challenging friction and forces question

[hibachii]

Homework Statement

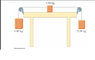
Three objects are connected on the table as shown in Figure P5.46 (a block of mass 1kg on a table is connected by two strings. The ends of the string each have a block hanging from it off the table, one of mass 4kg and one of mass 2kg. The strings are attached to a pulley system)
coefficient of kinetic friction between the block of mass m2
and the table is 0.350.
The objects have masses of m1
= 4.00 kg, m2
= 1.00 kg and m3
= 2.00 kg, and the
pulleys are frictionless. (a) Draw free-body diagrams of each of the objects. (b)
Determine the acceleration of each object and their directions. (c) Determine the
tensions in the two cords. What if? (d) If the tabletop were smooth, would the
tensions increase, decrease or stay the same? Explain.

Homework Equations

Figure P5.46 (in attachment)

The Attempt at a Solution

I have attempted a) and have no problem with it but it is b) and c) that is troubling me.
for b) i have written sum of all forces in the vertical direction is equal to 0(upwards positive). then i have input all the vertical forces for mass 1, T- mg=ma=0. I am stuck as i have two unknowns. please help!

 

[Doc Al]

for b) i have written sum of all forces in the vertical direction is equal to 0(upwards positive).

then i have input all the vertical forces for mass 1, T- mg=ma=0. I am stuck as i have two unknowns.

Why are you setting the acceleration equal to zero?

Write separate force equations for each mass then solve together.

 

[hibachii]

but then if i write separate force equations and solve together the acceleration would be the same for each mass wouldn't it? but it says to find acceleration of each mass. I am really confused :?

 

[Doc Al]

but then if i write separate force equations and solve together the acceleration would be the same for each mass wouldn't it? but it says to find acceleration of each mass.

The masses are connected by the strings. They will all have the same acceleration (the same magnitude, but different directions, of course).

 

[hibachii]

what are the force equations? i have no idea.

 

[Doc Al]

what are the force equations? i have no idea.

Do the same thing you did for mass 1: Write equations expressing Newton's 2nd law. (Don't set the acceleration equal to zero, though.) Make sure you do part (a) first: you'll need to know the forces acting on each mass.