zwierz
- 334
- 62
I composed a problem and propose it here. I know the solution so it just for fun of the participants.
There is a cylindrical bobbin of radius ##r##; the bobbin rotates about its central axis with angular velocity ##\omega=const>0##. An inextensible weightless string is coiled around the bobbin. The string is very thin and very long. On a free end of the string there is a point mass ##m##. Let ##l=l(t)## stand for the length of the free part of the string. There is no gravity.
Initially the value ##l_0=l(0)>0## and the velocity ##v=\frac{d}{dt} l\mid_{t=0}## are given. Moreover it is known that ##-\omega r<v<0##. Find minimal value of the function ##l(t)## that is ##\min_{t\ge 0}l(t)## -- ?.
We consider motion such that the string remains strained for all time
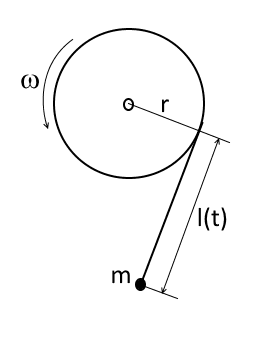
There is a cylindrical bobbin of radius ##r##; the bobbin rotates about its central axis with angular velocity ##\omega=const>0##. An inextensible weightless string is coiled around the bobbin. The string is very thin and very long. On a free end of the string there is a point mass ##m##. Let ##l=l(t)## stand for the length of the free part of the string. There is no gravity.
Initially the value ##l_0=l(0)>0## and the velocity ##v=\frac{d}{dt} l\mid_{t=0}## are given. Moreover it is known that ##-\omega r<v<0##. Find minimal value of the function ##l(t)## that is ##\min_{t\ge 0}l(t)## -- ?.
We consider motion such that the string remains strained for all time
Last edited by a moderator: