highschoboy004
- 15
- 3
- Homework Statement
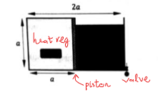
- A rectangular cuboid is made up of two identical cubes which have side length a = 10 cm. The cubes are separated by a frictionless piston of negligible mass in the middle. The cube on the left contains gas which has initial temperature of 27 degree Celsius and initial pressure 4x10^5 N/m2. The cube on the right is full of water. We then open the valve to drain the water at a constant rate of 10cm3/s, if we are to keep the piston still then at what rate must we lower the gas temperature (°C/s)(using the heat regulator)?
- Relevant Equations
- nRT=pV
Last edited: