A man hangs from a hole, Horizontal pulley

[Skilen]

I

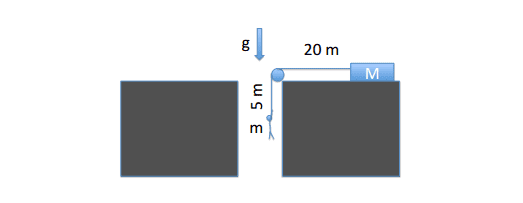
1. A man of mass m = 80.0 kg hangs from a rope down into a hole. The rope goes over a massless pulley and is connected to a block of rock of mass M = 200 kg, which is lying on a frictionless horizontal surface. The distance between pulley and man is 5.00 m; between pulley and block 20.0 m.

a) What is the acceleration of the man (and rock)? How long does it take before the block crashes into the pulley, rips it off and everything plunges into the hole? The block and man start from rest.

b) Instead of just hanging there, the man decides to climb up the rope while everything is moving. Is it possible for him to get enough (constant) acceleration to get to the pulley and to safety, before the block hits the pulley? What is the acceleration of him and of the block in the case where he just makes it?

Homework Equations

F=m*a ; Newtons Second Law.
m_1 = 200kg
m_2 = 80kg
distance between pulley and rock = 20m
distance between man and pulley = 5m

The Attempt at a Solution

For a) I used the Newtons Second Law to make an equation relative to acceleration [ a=(m_2*g)/(m_1+_2) ] and got the answer 2,8m/s^2.
For a) to find the time from rocks start position to the pulley, I found the ewuation D=a*(t^2/2), which in the end turns out to be: t=sqrt(2D/a) which gives me 3,778 sec.

For task b) however, i can't figure out a smart way to find the relative time and acceleration that proves if he makes it or not. Tried it several times, but haven't found anything. This is what need help with. Thanks to all response on beforehand :)

 

[haruspex]

Suppose the man accelerates upwards at rate a, relative to the ground. What is the tension in the rope?

 

[Skilen]

Suppose the man accelerates upwards at rate a, relative to the ground. What is the tension in the rope?

I suppose you put in the mans weight relative to the ground. Which in this case becomes:

T=m*g = 80kg*9,8m/s^2= 784N. Or am I totaly lost here?

 

[stockzahn]

I suppose you put in the mans weight relative to the ground. Which in this case becomes:

T=m*g = 80kg*9,8m/s^2= 784N. Or am I totaly lost here?

That would be the case, if he'd just hang there. Considering he tries to climb up, there is an additional acceleration to be added.

 

[1988Teun]

I totally agree with your answer to a) !
for b), I would say that following Newton's 3rd law, the same force F_pull you exert on the rope to pull up, pulls the block towards you. Here we have an additional acceleration a_pullBlock of the block towards the pulley and another one a_pullUp of you climbing up the robe, where:

F_pull= a_pullBlock * m_1 = a_pullUp * m_2

now you want to be at the pulley at the same time as the block. You accelerate there with a_pullUp and have to cover 5 m, while the bock accelerates with a (from a) ) + a_pullBlock to cover 20 meters. The time to cover (as you showed in a: t=sqrt(2D/a) ), thus:

t=sqrt( 2 * 5 / a_pullUp)=sqrt( 2 * 20 / ( a_pullBlock + a)

 

[Skilen]

I totally agree with your answer to a) !
for b), I would say that following Newton's 3rd law, the same force F_pull you exert on the rope to pull up, pulls the block towards you. Here we have an additional acceleration a_pullBlock of the block towards the pulley and another one a_pullUp of you climbing up the robe, where:

F_pull= a_pullBlock * m_1 = a_pullUp * m_2

now you want to be at the pulley at the same time as the block. You accelerate there with a_pullUp and have to cover 5 m, while the bock accelerates with a (from a) ) + a_pullBlock to cover 20 meters. The time to cover (as you showed in a: t=sqrt(2D/a) ), thus:

t=sqrt( 2 * 5 / a_pullUp)=sqrt( 2 * 20 / ( a_pullBlock + a)

How do i find the values of a_pullUp and a_pullBlock? Can I just adjust the equation where the current value of t is 3,778 seconds??

 

[1988Teun]

How do i find the values of a_pullUp and a_pullBlock? Can I just adjust the equation where the current value of t is 3,778 seconds??

well you know have 2 equations:
a_pullBlock * m_1 = a_pullUp * m_2
sqrt( 2 * 5 / a_pullUp)=sqrt( 2 * 20 / ( a_pullBlock + a)

with two unknows: a_pullBlock, a_pullUp so you can solve to find a_pullUp which you can plug in t=sqrt( 2 * 5 / a_pullUp) to find t :)

 

[Skilen]

well you know have 2 equations:
a_pullBlock * m_1 = a_pullUp * m_2
sqrt( 2 * 5 / a_pullUp)=sqrt( 2 * 20 / ( a_pullBlock + a)

with two unknows: a_pullBlock, a_pullUp so you can solve to find a_pullUp which you can plug in t=sqrt( 2 * 5 / a_pullUp) to find t :)

Ahh, I see it now. Thank you, made my day. :)

 

[haruspex]

I totally agree with your answer to a) !
for b), I would say that following Newton's 3rd law, the same force F_pull you exert on the rope to pull up, pulls the block towards you. Here we have an additional acceleration a_pullBlock of the block towards the pulley and another one a_pullUp of you climbing up the robe, where:

F_pull= a_pullBlock * m_1 = a_pullUp * m_2

now you want to be at the pulley at the same time as the block. You accelerate there with a_pullUp and have to cover 5 m, while the bock accelerates with a (from a) ) + a_pullBlock to cover 20 meters. The time to cover (as you showed in a: t=sqrt(2D/a) ), thus:

t=sqrt( 2 * 5 / a_pullUp)=sqrt( 2 * 20 / ( a_pullBlock + a)

Teun, I know you are just trying to be helpful, but the way this forum works is that we give just sufficient nudges in the right direction. The aim is that the problem poster is led to think in the right way and solves it for him or her self. I judge that you spelled out a bit too much here.
(There is a Report button I should use, but I will refrain on this occasion.)

Anyway, I'm not entirely sure your solution is correct. Is your a_pullup relative to the ground or relative to the rope? You added a, the original acceleration, to a_pullblock but did not subtract a from a_pullup, so there appears to be an inconsistency.

Skilen, I suggest you start with a clearly defined unknown (maybe the acceleration of the man relative to the rope, or the tension in the rope), and try working it through from there for yourself using the usual free body analysis for each object.

 

[Skilen]

Teun, I know you are just trying to be helpful, but the way this forum works is that we give just sufficient nudges in the right direction. The aim is that the problem poster is led to think in the right way and solves it for him or her self. I judge that you spelled out a bit too much here.
(There is a Report button I should use, but I will refrain on this occasion.)

Anyway, I'm not entirely sure your solution is correct. Is your a_pullup relative to the ground or relative to the rope? You added a, the original acceleration, to a_pullblock but did not subtract a from a_pullup, so there appears to be an inconsistency.

Skilen, I suggest you start with a clearly defined unknown (maybe the acceleration of the man relative to the rope, or the tension in the rope), and try working it through from there for yourself using the usual free body analysis for each object.

It didnt lead me directly to the answer. I didnt directly do as teun said, but rather worked me through to the answer. Kinda like the direction you put me towards. Anyway, It is solved, thank you all so much for the help :)

 

[haruspex]

It didnt lead me directly to the answer. I didnt directly do as teun said, but rather worked me through to the answer. Kinda like the direction you put me towards. Anyway, It is solved, thank you all so much for the help :)

Glad to hear it, and well done.