A man is driving around a curve rather quickly one day

[HappyFlower]

Homework Statement

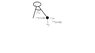
a man is driving around a curve rather quickly one day at 21.2m/s. He has an object hanging from his mirror that makes an angle of 36.4 wih respect to vertical as he goes around the curve. What is the radius of the curve?

Homework Equations

The Attempt at a Solution

I set up this but i don't know where to start.

 

[haruspex]

You have written mg sin(θ) and mg cos(θ) on your diagram, but I cannot tell what you think these represent.

 

[HappyFlower]

You have written mg sin(θ) and mg cos(θ) on your diagram, but I cannot tell what you think these represent.

I was just making a diagram, don't know where to start.

 

[jbriggs444]

I was just making a diagram, don't know where to start.

I am not sure that I agree with your choice in separating gravity into components so soon. But let us see where it leads.

You've identified two forces (the components of gravity) and one acceleration on the object so far. Are there any other forces?

 

[HappyFlower]

would i split up the tension instead that is in the string?

 

[jbriggs444]

would i split up the tension instead that is in the string?

If it were me, I'd likely have split tension into components. But let us see how far we can go having split up gravity instead (see note below).

Can you write down any equations relating mg cos(θ), mg sin(θ), tension and acceleration? (I am guessing that ∝ is intended to denote radial acceleration).

Note:

There are two forces and one acceleration on the object. Gravity, tension and centripetal acceleration. Gravity and centripetal acceleration are at right angles. If you decide to use a coordinate system at an angle to the one then it will be at an angle to the other as well. If you decide to use a coordinate system that is aligned with the one, then it will be aligned with the other as well. That's two simplifications. By contrast, if you align your coordinate system with the angle of the string you only get one simplification.

Either coordinate system will work, but I'm betting that one choice is easier than the other.​