- #1
yuiop
- 3,962
- 20
Right angle lever paradox.
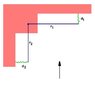
This paradox has long been a thorn in the side of relativity. In 1909 Lewis and Tolman analysed the behaviour of a right angled lever with balanced forces with relative motion. They noticed there would be a potential imbalance as the arm parallel to the direction of motion would length contract. They proposed that the force transverse to the direction of motion should increase to compensate for the length contracting arm. Later it was shown that the transformation of force does exactly the opposite and the force actually decreases, making it difficult to explain why if the lever does not rotate in the rest frame, why does it not rotate in the moving frame? So the lever paradox was born.
Proposed solutions to date include a energy flow into the lever that counteracts the apparent imbalance of a right angle lever with relative motion (The Von Laue energy current) and an “internal torque” that exactly balances the external torque.
http://scitation.aip.org/getabs/servlet/GetabsServlet?prog=normal&id=AJPIAS000043000007000615000001&idtype=cvips&gifs=yes
http://panda.unm.edu/Courses/Finley/P495/TermPapers/relangmom.pdf
Another proposed solution is that static forces transform in a different way to dynamic forces. http://www.springerlink.com/content/n6573281634614q2/
Einstein did not help when he stated relativity is not about statics but about time and motion.
To the layperson these solutions are non intuitive and appear a bit too convenient and ad hoc. In fact a search on the internet reveals that this paradox has lead many to believe there is something wrong with the force transformations or with relativity itself.
An example is this paper http://www.wbabin.net/science/ricker12.pdf that concludes that the accepted Lorentz transformation for transverse force is wrong.
Early in the paper the author substitutes x=0 in the Lorentz transformation [tex] t\prime =(t-vx/c^2)/ \sqrt{1-v^2/c^2}[/tex] to obtain [tex] t =t\prime\sqrt{1-v^2/c^2}[/tex]. Clearly a big mistake. If x is set to zero, then there is no motion in the unprimed frame and v can only take the value zero. His result is also at odds with time dilation measured in experiments.
I would like to propose a new solution to the Right Angle Lever paradox that I feel is more intuitive and odes not require tampering with any of the classical force transformations of Special Relativity.
The new solution requires an introduction of a concept I call a geared lever.
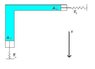
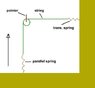
The geared lever is here defined as a gear box with two equal length levers connected to the input and output shafts of the gear box. The gears are hidden in a “black box” that cannot be opened and we observe the behaviour of the input and output levers when forces are applied.
Li = length of input arm.
Lo = Length of output arm.
Ai = Angular displacement of input arm.
Ao = Angular displacement of output arm.
Di = Tangential displacement of input arm.
Do = Tangential displacement of output arm.
MA = Mechanical advantage (Output force/input force)
Classic lever
A) Li/Lo = MA
B) Ai/Ao = 1
C) Di/Do = MA
Geared lever
A) Li/Lo = 1
B) Ai/Ao = MA
C) Di/Do = MA
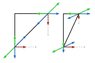
From the above it can be seen that only the ratio Di/Do can be applied generally to both classical levers and geared levers to obtain the correct mechanical advantage. When it is realized that the right angle lever in relative motion behaves as a geared lever, the toques are balanced and there is no paradox. When the right angle lever is rotated by a small angle in the rest frame of the lever, the tip of the transverse arm moves less than the tip of the arm parallel to the motion. It turns out that the distance moved by the tip of the transverse arm is less by [tex]\sqrt{1-v^2/c^2}[/tex] and the mechanical advantage of the lever due to the ratio of the tip displacements exactly compensates for the reduced transverse force applied to the parallel lever. The distance moved by the transverse tip is effectively length contracted. (By definition of the geared lever law, the lengths of the arms is irrelevant as far as mechanical advantage is concerned.)
In the relativistic right angle lever the reduced displacement of the transverse arm and the reduced force acting on the parallel arm means energy is conserved since one definition of energy is force multiplied by the distance the force acts through.
It should also be noted that the when the right angle lever is rotated by some small angle in the rest frame that the two arms rotate through different angles in the moving frame and the angle between the arms does not remain a right angle. I hope I have shown that the relativistic right angle lever has more in common with a "geared lever" than a classical lever and that the ratio of the tip displacements is a more generally applicable “law of the lever” than the simple ratio of the lever arm lengths.
This paradox has long been a thorn in the side of relativity. In 1909 Lewis and Tolman analysed the behaviour of a right angled lever with balanced forces with relative motion. They noticed there would be a potential imbalance as the arm parallel to the direction of motion would length contract. They proposed that the force transverse to the direction of motion should increase to compensate for the length contracting arm. Later it was shown that the transformation of force does exactly the opposite and the force actually decreases, making it difficult to explain why if the lever does not rotate in the rest frame, why does it not rotate in the moving frame? So the lever paradox was born.
Proposed solutions to date include a energy flow into the lever that counteracts the apparent imbalance of a right angle lever with relative motion (The Von Laue energy current) and an “internal torque” that exactly balances the external torque.
http://scitation.aip.org/getabs/servlet/GetabsServlet?prog=normal&id=AJPIAS000043000007000615000001&idtype=cvips&gifs=yes
http://panda.unm.edu/Courses/Finley/P495/TermPapers/relangmom.pdf
Another proposed solution is that static forces transform in a different way to dynamic forces. http://www.springerlink.com/content/n6573281634614q2/
Einstein did not help when he stated relativity is not about statics but about time and motion.
To the layperson these solutions are non intuitive and appear a bit too convenient and ad hoc. In fact a search on the internet reveals that this paradox has lead many to believe there is something wrong with the force transformations or with relativity itself.
An example is this paper http://www.wbabin.net/science/ricker12.pdf that concludes that the accepted Lorentz transformation for transverse force is wrong.
Early in the paper the author substitutes x=0 in the Lorentz transformation [tex] t\prime =(t-vx/c^2)/ \sqrt{1-v^2/c^2}[/tex] to obtain [tex] t =t\prime\sqrt{1-v^2/c^2}[/tex]. Clearly a big mistake. If x is set to zero, then there is no motion in the unprimed frame and v can only take the value zero. His result is also at odds with time dilation measured in experiments.
I would like to propose a new solution to the Right Angle Lever paradox that I feel is more intuitive and odes not require tampering with any of the classical force transformations of Special Relativity.
The new solution requires an introduction of a concept I call a geared lever.
The geared lever is here defined as a gear box with two equal length levers connected to the input and output shafts of the gear box. The gears are hidden in a “black box” that cannot be opened and we observe the behaviour of the input and output levers when forces are applied.
Li = length of input arm.
Lo = Length of output arm.
Ai = Angular displacement of input arm.
Ao = Angular displacement of output arm.
Di = Tangential displacement of input arm.
Do = Tangential displacement of output arm.
MA = Mechanical advantage (Output force/input force)
Classic lever
A) Li/Lo = MA
B) Ai/Ao = 1
C) Di/Do = MA
Geared lever
A) Li/Lo = 1
B) Ai/Ao = MA
C) Di/Do = MA
From the above it can be seen that only the ratio Di/Do can be applied generally to both classical levers and geared levers to obtain the correct mechanical advantage. When it is realized that the right angle lever in relative motion behaves as a geared lever, the toques are balanced and there is no paradox. When the right angle lever is rotated by a small angle in the rest frame of the lever, the tip of the transverse arm moves less than the tip of the arm parallel to the motion. It turns out that the distance moved by the tip of the transverse arm is less by [tex]\sqrt{1-v^2/c^2}[/tex] and the mechanical advantage of the lever due to the ratio of the tip displacements exactly compensates for the reduced transverse force applied to the parallel lever. The distance moved by the transverse tip is effectively length contracted. (By definition of the geared lever law, the lengths of the arms is irrelevant as far as mechanical advantage is concerned.)
In the relativistic right angle lever the reduced displacement of the transverse arm and the reduced force acting on the parallel arm means energy is conserved since one definition of energy is force multiplied by the distance the force acts through.
It should also be noted that the when the right angle lever is rotated by some small angle in the rest frame that the two arms rotate through different angles in the moving frame and the angle between the arms does not remain a right angle. I hope I have shown that the relativistic right angle lever has more in common with a "geared lever" than a classical lever and that the ratio of the tip displacements is a more generally applicable “law of the lever” than the simple ratio of the lever arm lengths.
Last edited by a moderator: