lloydthebartender
- 50
- 1
- Homework Statement
- I found the question here (https://isaacphysics.org/questions/three_cylinders?board=c197ce8f-5684-418a-9a4b-de5cb43b3da6).
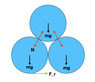
Two rough cylinders, each of mass m and radius r are placed parallel to each other on a rough surface with their curved sides touching. A third equivalent cylinder is balanced on top of these two, with its axis running in the same direction.
For this setup to be stable, what is the minimum coefficient of friction between the horizontal surface and the cylinders? Give your answer to three significant figures.
- Relevant Equations
- ##F_r=(\mu)R##
Firstly the normal reaction force of the bottom cylinder is ##R## and because all three cylinders are identical ##2R=3mg##, and so the frictional force is going to be ##F_r={(3mg)/(2}{\mu})##. I don't use this, though.
If the normal reaction force between the top cylinder and one of the bottoms cylinder is ##N##, then by the centres of the three cylinders making an equilateral triangle, we can say ##N=(1/2)mg##. This reaction force provides a horizontal and vertical force on the bottom cylinder, where the horizontal force is equal to the frictional force. The vertical force adds to the weight of the bottom cylinder.
Because the angle ##N## makes with the vertical is 60 degrees, the vertical component is ##(\sqrt3/4)mg## and the horizontal is ##(1/4)mg##. So finally ##R=mg+(\sqrt3/4)mg## and ##F_r=(1/4)mg##, and I equate for ##\mu## to get 0.174, which isn't right.
I can't put my finger on where I went wrong so help is appreciated!
If the normal reaction force between the top cylinder and one of the bottoms cylinder is ##N##, then by the centres of the three cylinders making an equilateral triangle, we can say ##N=(1/2)mg##. This reaction force provides a horizontal and vertical force on the bottom cylinder, where the horizontal force is equal to the frictional force. The vertical force adds to the weight of the bottom cylinder.
Because the angle ##N## makes with the vertical is 60 degrees, the vertical component is ##(\sqrt3/4)mg## and the horizontal is ##(1/4)mg##. So finally ##R=mg+(\sqrt3/4)mg## and ##F_r=(1/4)mg##, and I equate for ##\mu## to get 0.174, which isn't right.
I can't put my finger on where I went wrong so help is appreciated!