MBrain
- 3
- 0
Hello there :) First I'm sorry for my English it might be kinda bad !
I Have a little question about Weight and Pressure, Hope this is the right place.
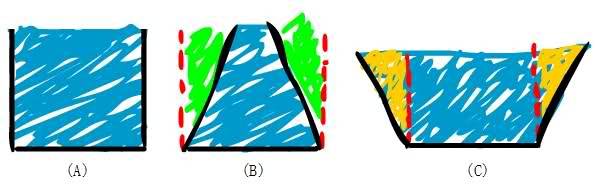
Here in this image we have 3 samples, A, B and C.
They are 3 different types of shapes fulled with a liquid (let's say water)
Talking about the physical pressure on the bottom of every shape :-
In Sample (A) we can see that Weight = Pressure.
In Sample (B) we can see that Weight < Pressure.
In Sample (C) we can see that Weight > Pressure.
Where did we get the extra pressure in the sample (B) ? It's like we create that green area from nowhere!
And where did the extra weight go in the sample (C) ? It's like we lost that orange area and it's nothing!
Hope I can fine the answer, Thank you :) !
I Have a little question about Weight and Pressure, Hope this is the right place.
Here in this image we have 3 samples, A, B and C.
They are 3 different types of shapes fulled with a liquid (let's say water)
Talking about the physical pressure on the bottom of every shape :-
In Sample (A) we can see that Weight = Pressure.
In Sample (B) we can see that Weight < Pressure.
In Sample (C) we can see that Weight > Pressure.
Where did we get the extra pressure in the sample (B) ? It's like we create that green area from nowhere!
And where did the extra weight go in the sample (C) ? It's like we lost that orange area and it's nothing!
Hope I can fine the answer, Thank you :) !