- #1
Aslet
- 20
- 1
Homework Statement
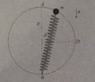
I uploaded the image of the system to have a visual example. : )
A point mass ## m ## connected to a spring is bounded to move on a circular guide with radius ## R ## without friction. The guide is fixed to a vertical plane and the other extremity of the spring is attached at point ## B ##, which is the bottom of the guide. The rest length of the spring is ## 2 R ##. Initially the mass is in the point ## A ## and at ## t = 0 ## it begins to move with a negligible velocity
1) Knowing that the mass richeas the point ## D ## with ## v=0 ##, find the spring constant ## k ##;
2) Find the acceleration ## a_D ## and the reaction ## N_D ## of the guide at point ## D ##;
3) Let ## \theta ## be the angle between the spring and the vertical. Find the angle at which the velocity is maximum.
The Attempt at a Solution
1) I use the energy conservation. First of all I choose the zero of the potential at point ## A ## such that the initial energy is equal to zero. Then I set that equal to the energy at point ## D ##, knowing from the geometry of the system that the length of the spring in this point is ## \sqrt 2 R ##:
$$ 0 = k R^2 - m g R \quad \Longrightarrow \quad k = \dfrac { m g }{ R } $$
2) I chose the frame centered in ## B ##. Because the reaction is always perpendicular to the guide, at point ## D ## the reaction force has only a component along the ## x ## axis and then:
$$ N_D = k R = m g $$
because the mass is not moving along ## x ## in this position.
Along the positive direction of ## y ## axis there is an acceleration which is given by:
$$ m a_D - mg = kR \quad \Longrightarrow \quad a_D = 2 g $$
where i have substituted the value of ## k ##
3) Up to now, the only thing that I have in mind is that the velocity is maximum when the acceleration is equal to zero. So I tried to write down that the sum of the forces along both axes is zero but I need another condition. I thought that maybe I have also to impose the minimum potential energy but I am not so sure.
Can you please give me any hint? Also, do you think that the answers to questions 1 and 2 are correct? Thank you in advance. : )


 , you do a similar thing when you want to study a termodynamic system and its stable states with the Landau theory, right?
, you do a similar thing when you want to study a termodynamic system and its stable states with the Landau theory, right?