A stirring Rod in a hemispherical bowl

  • Thread starter Thread starter loisse
  • Start date Start date
  • Tags Tags
    Rod
loisse
Messages
1
Reaction score
0
[. Homework Statement
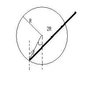
Once you place a stirring rod (uniform density) of length 2R in a frictionless hemispherical bowl of radius R, it always comes to rest after one of its ends makes an angle of θ0 with respect to the vertical
(diagram attached)

a) derive a root equation for f(θ)=0 that can be used to solve for θ0]
b) what is the numerical value of θ0?


2. Homework Equations

none

3. The Attempt at a Solution

sorry but I don't know the concepts that can be used to solve such problem. please help me. Thank you very much
we are currently taking up oscillations and i tried to relate it but i end up totally messed up.
 

Attachments

  • s.JPG
    s.JPG
    5.4 KB · Views: 560
Physics news on Phys.org
The rod is touched by the bowl at two points where there is a radial force on the rod. Draw a free body diagram and wrilte the force and torque equations.
Include mg at the center of the rod.
 

Thread 'Initial conditions for orbits around a wormhole'

Hi, I had an exam and I completely messed up a problem. Especially one part which was necessary for the rest of the problem. Basically, I have a wormhole metric: $$(ds)^2 = -(dt)^2 + (dr)^2 + (r^2 + b^2)( (d\theta)^2 + sin^2 \theta (d\phi)^2 )$$ Where ##b=1## with an orbit only in the equatorial plane. We also know from the question that the orbit must satisfy this relationship: $$\varepsilon = \frac{1}{2} (\frac{dr}{d\tau})^2 + V_{eff}(r)$$ Ultimately, I was tasked to find the initial...
View full post »

Thread 'Help to convert units of a simple formula'

The value of H equals ## 10^{3}## in natural units, According to : https://en.wikipedia.org/wiki/Natural_units, ## t \sim 10^{-21} sec = 10^{21} Hz ##, and since ## \text{GeV} \sim 10^{24} \text{Hz } ##, ## GeV \sim 10^{24} \times 10^{-21} = 10^3 ## in natural units. So is this conversion correct? Also in the above formula, can I convert H to that natural units , since it’s a constant, while keeping k in Hz ?
View full post »

Similar threads

Multipole Expansion of a Thin Rod: How to Derive the Potential?
Replies
2
Views
5K
When Will the Rod Fall without Slipping?
Replies
1
Views
4K
Simple harmonic motion of a charged particle in a rod
Replies
9
Views
6K
Force of magnetic attraction between hemispheres
Replies
2
Views
4K
Electrostatic Interaction Energy of a Rod and a Ring
Replies
12
Views
4K
How Does a Rod Attached to a Spring Undergo Simple Harmonic Motion?
Replies
3
Views
3K
Particle mass atop frictionless hemisphere w/ extra force
Replies
3
Views
1K
What is the angle of equilibrium for a rod in a hemispherical bowl?
Replies
3
Views
5K
To find the weight of a hemisphere
Replies
13
Views
2K
What are the generalized coordinates for the suspended rod Lagrangian?
Replies
1
Views
3K

Hot Threads

Recent Insights

Back
Top