- #1
charger9198
- 60
- 0
For the circuit given in the power factor is 0.72 lagging and
the power dissipated is 375 W.
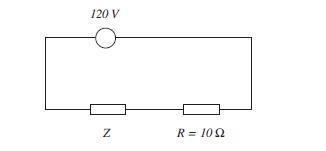
Determine the:
(1) apparent power
(2) reactive power
(3) the magnitude of the current flowing in the circuit
(4) the value of the impedance Z and state whether circuit is inductive or
capacitive.
(1) Apparent power = True power / Power Factor (S=P/pf)
= 375 / 0.72
= 520.8333 VA
(2) Reactive Power = SQRT (apparent power^2) - (True Power^2)
= SQRT (520.8333^2)-(375^2)
= SQRT (130642.3264)
= 361.4448 VAR
(3) Magnitude of Current
Power= Voltage*Current *Power factor (P=V*I*pf)
375 = 120*I*0.72
I = P/(V*pf)
I = 375/(120*0.72)
I = 4.34 A
(4) Total ohms = Voltage/Current
= 120/4.34
=27.6498 ohms (minus 10)
z = 17.65 ohms
The power factor is lagging within the circuit therefore the the virvuit is inductive
Am i on the right lines here? or is there a better way of calculating the above results
the power dissipated is 375 W.
Determine the:
(1) apparent power
(2) reactive power
(3) the magnitude of the current flowing in the circuit
(4) the value of the impedance Z and state whether circuit is inductive or
capacitive.
(1) Apparent power = True power / Power Factor (S=P/pf)
= 375 / 0.72
= 520.8333 VA
(2) Reactive Power = SQRT (apparent power^2) - (True Power^2)
= SQRT (520.8333^2)-(375^2)
= SQRT (130642.3264)
= 361.4448 VAR
(3) Magnitude of Current
Power= Voltage*Current *Power factor (P=V*I*pf)
375 = 120*I*0.72
I = P/(V*pf)
I = 375/(120*0.72)
I = 4.34 A
(4) Total ohms = Voltage/Current
= 120/4.34
=27.6498 ohms (minus 10)
z = 17.65 ohms
The power factor is lagging within the circuit therefore the the virvuit is inductive
Am i on the right lines here? or is there a better way of calculating the above results