thejinx0r
- 27
- 0
Homework Statement
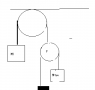
Mass M1 and M2 are connected to a system of strings and pulleys as shown. The strings are massless and inextensible and the pulleys are massless and frictionless. Find the acceleration of M1.
(image attached.
just to clarify the image, the upper left pulley is fixed to the ceiling and the bottom center black box is a fixed point on the floor. Imagine everything is perfectly centered as my skills on Paint are not so great)
Homework Equations
F=ma
The Attempt at a Solution
So, I do my FBD's for the 2 masses. Straightforward: gravity pointing down, tension pointing up.
It starts to get tricky on the pulley I labeled P.
Clearly, it will start to accelerate at some point. So, my FBD on it was T1 pointing up where T1 is the tension of the string due to M1. For the force pointing down, I said there would have to be at least 2*T2 because the first one comes from the mass M2 and the other comes from the "normal" force of the stationary hook (my black box).
The problem is the pulley is massless and I'm not sure how to treat it.
So I said treated the second pulley as a system. So it would have a mass of m2, with forces T1 pointing up, and 2*T2 pointing down.
Now, I have 3 equations, 3 unkowns. So I solve.
The problem was taken from Kleppner and Kolenkow, Q2.12 and the hint is : if M1=M2, then a=g/5.
And I get a=-g/2. So there must be something wrong with the way I treated the pulley.