- #1
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Calculating Acceleration with Tension: A Troubleshooting Guide
- Thread starter user5
- Start date
-
- Tags
- Acceleration Tension
In summary, the conversation discusses a problem with calculating acceleration and the use of angles in the formula. It is suggested that the incorrect use of angles may have led to the wrong answer. The importance of correctly placing the angle is also mentioned and it is noted that acceleration can never be infinite in the real world. The relationship between acceleration and a constant force is also discussed.
Physics news on Phys.org
- #2
voko
- 6,054
- 391
You did not go wrong anywhere, but you did not finish. You have some angle in your formula, while the expected result does not have any.
- #3
user5
- 38
- 0
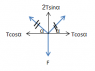
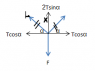
I have Tx=(FCOSα)/(2SINα)=(F)/(2TANα)=[F(L2-X2)0.5)]/2X
I have the wrong answer:(
I have the wrong answer:(
- #4
voko
- 6,054
- 391
You obviously used the wrong sides of the triangle to compute the tangent function. Think about that again. If you come to the same result again, post your thoughts here, and we will discuss.
- #5
- #6
voko
- 6,054
- 391
Which side is x? How is it related with the angle?
- #7
- #8
voko
- 6,054
- 391
x is the perpendicular distance from the line of F. Is that the case on your diagram?
- #9
user5
- 38
- 0
Thus it is going to be tanα=(L2-X2)0.5/X? With 2Tsinα=F it seems to give the right answer, however in the "student solution" they refer to that problem as having 2Tcosα=F, Am I right this time?
Does it matter where I decide to place α ?
Does it matter where I decide to place α ?
Last edited:
- #10
user5
- 38
- 0
1. From the start x=L thus is the acceleration infinite?
2. Is ax changing while F is constant?
2. Is ax changing while F is constant?
- #11
Cbray
- 134
- 0
The notation in your working hurts my brain.
- #12
voko
- 6,054
- 391
user5 said:Thus it is going to be tanα=(L2-X2)0.5/X? With 2Tsinα=F it seems to give the right answer, however in the "student solution" they refer to that problem as having 2Tcosα=F, Am I right this time?
Does it matter where I decide to place α ?
Obviously, there are two angles that you can use, but the end result should be the same.
user5 said:1. From the start x=L thus is the acceleration infinite?
Nothing ever gets infinite in the real world. If you get something infinite in a problem, that means that its mathematical model becomes invalid.
2. Is ax changing while F is constant?
It depends on the angle, so, yes.
- #13
user5
- 38
- 0
voko, I'm grateful to you for your help!
1. What is acceleration with tension?
Acceleration with tension refers to the change in velocity of an object as a result of the force of tension acting on it. This can occur when an object is being pulled or stretched by a force, causing it to accelerate in the direction of the force.
2. How is acceleration with tension calculated?
In order to calculate acceleration with tension, you will need to know the mass of the object that is being pulled or stretched, as well as the force of tension acting on it. The formula for acceleration with tension is a = F/m, where a is the acceleration, F is the force of tension, and m is the mass of the object.
3. What factors affect acceleration with tension?
There are several factors that can affect acceleration with tension, including the mass of the object, the force of tension, and the direction of the force. Additionally, the presence of any other forces acting on the object can also impact its acceleration with tension.
4. How does acceleration with tension relate to Newton's laws of motion?
Acceleration with tension is closely related to Newton's laws of motion, specifically the second law which states that the acceleration of an object is directly proportional to the net force acting on it and inversely proportional to its mass. This means that as the force of tension increases, the acceleration of the object will also increase, and vice versa.
5. Can acceleration with tension be negative?
Yes, acceleration with tension can be negative. This occurs when the force of tension is acting in the opposite direction of the object's motion, causing it to decelerate or slow down. In this case, the acceleration would be represented by a negative value in the formula a = F/m.
Similar threads
- Replies
- 38
- Views
- 1K
-
Introductory Physics Homework Help
- Replies
- 4
- Views
- 163
- Replies
- 43
- Views
- 2K
-
Introductory Physics Homework Help
- Replies
- 10
- Views
- 1K
- Replies
- 52
- Views
- 633
-
Introductory Physics Homework Help
- Replies
- 15
- Views
- 399
-
Introductory Physics Homework Help
- Replies
- 13
- Views
- 231
-
Introductory Physics Homework Help
- Replies
- 6
- Views
- 2K
-
Introductory Physics Homework Help
- Replies
- 13
- Views
- 1K
-
Introductory Physics Homework Help
- Replies
- 23
- Views
- 2K
Share: