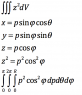SarahAlbert
- 10
- 0
Homework Statement
Use spherical coordinates to evaluate the integral over a sphere of radius R.
Homework Equations
The equation of my sphere would be x^2+y^2+z^2=R^2
Please see the attached file.
The Attempt at a Solution
I have attached a file to show my work so far. Evaluating the integral once it is set up should be fine, I'm concerned it's not set up correctly. Thank you.