- #1
- 8,520
- 16
This is an explanation and illustration of how different reference frames assign coordinates to points in space and time, which I wrote up a while ago on a different forum. I figure it might be interesting to people here, especially in terms of showing how two different observers can both see the other observer's clocks slowing down and rulers shrinking in relation to their own, without leading to any inconsistencies (the key is to understand how different reference frames also define simultaneity differently). Here it is:
A reference frame is really just a coordinate system for marking the location and time of different events. You can think of the physical basis of these coordinates in terms of each observer having a network of rulers and clocks spread throughout space, so if you imagine taking a picture of an event as it happens, its coordinates are defined by the markings on the ruler and the time on the clock right next to the event in the photo. Each observer uses a network of rulers and clocks which are at rest relative to himself. Clocks at different locations must all be synchronized, and in classical physics this would be pretty simple--you could just bring two clocks together to check that they're in sync, then move them to different positions. But time dilation due to movement makes sychronization a little trickier. Einstein's idea was that you could have each observer synchronize their own set of clocks using light signals--pick a point halfway between two clocks, send a flash of light from that point in both directions, and if both clocks read the same time when the light reaches them, they are considered synchronized. But unlike the Galilean frames used in classical physics, this means that the different Lorentzian frames used in relativity will not agree about simultaneity of pairs of events. For example, if an observer on a spaceship sees a flash of light go off in the middle of the ship, then he should synchronize clocks at the front and back of the ship by making sure they both read the same time when the light hits them. But for another observer who sees the ship moving, the back of the ship is moving towards the point where the flash happened and the front is moving away from that point, so his own network of clocks will be synchronized in such a way that the clock next to the event "light hits the back of the ship" will read an earlier time than the clock next to the event "light hits the front of the ship".
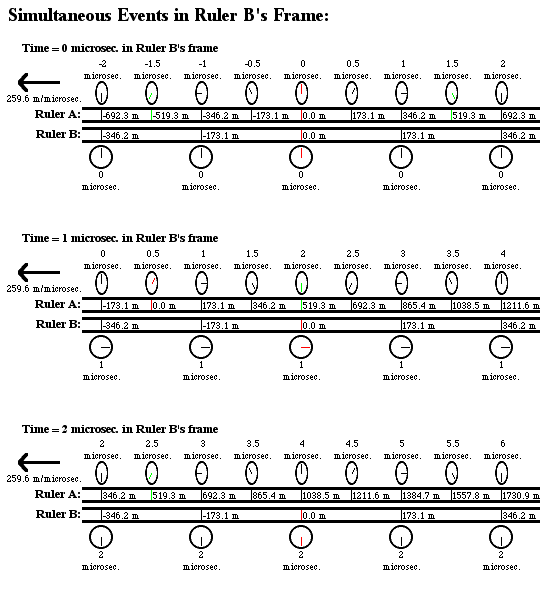
Here are some diagrams which may help explain how different reference frames could each see the other's rulers contracted and the other's times dilated without leading to any contradictions. In this example, we have two rulers with clocks mounted on them moving alongside each other, and in order to make the math work out neatly, the relative velocity of the two rulers is (square root of 3)/2 * light speed, or about 259.628 meters per microsecond. This means that each ruler will observe the other one’s clocks tick exactly half as fast as their own, and will see the other ruler's distance-markings to be squashed by a factor of two. Also, I have drawn the markings on the rulers at intervals of 173.085 meters apart—the reason for this is again just to make things work out neatly, it will mean that observers on each ruler will see the other ruler moving at 1.5 markings/microsecond relative to themselves, and that an observer on one ruler will see clocks on the other ruler that are this distance apart (as measured by his own ruler) to be out-of-sync by exactly 1 microsecond, some more nice round numbers.
Given all this, here is how the situation would look at 0 microseconds, 1 microsecond, and 2 microseconds, in the frame of ruler A:
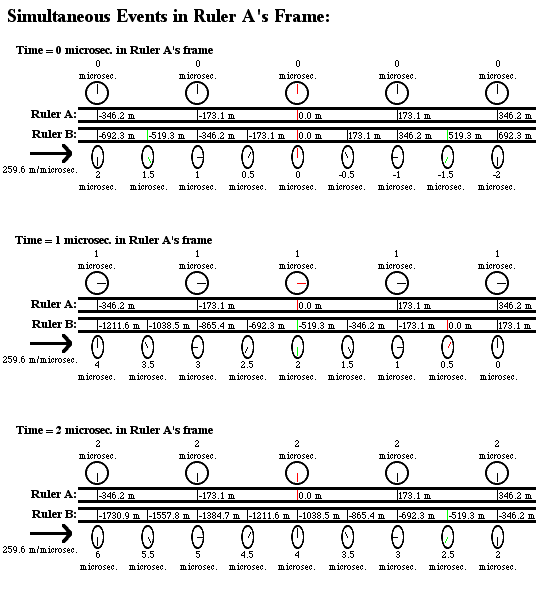
And here’s how the situation would look at 0 microseconds, 1 microsecond, and 2 microseconds, in the frame of ruler B:
Some things to notice in these diagrams:
1. in each ruler's frame, it is at rest while the other ruler is moving sideways at 259.6 meters/microsecond (ruler A sees ruler B moving to the right, while ruler B sees ruler A moving to the left).
2. In each ruler's frame, its own clocks are all synchronized, but the other ruler's clocks are all out-of-sync.
3. In each ruler's frame, each individual clock on the other ruler ticks at half the normal rate. For example, in the diagram of ruler A’s frame, look at the clock with the green hand on the -519.3 meter mark on ruler B--this clock first reads 1.5 microseconds, then 2 microseconds, then 2.5 microseconds. Likewise, in the diagram of ruler B’s frame, look at the clock with the green hand on the 519.3 meter mark on ruler A—this clock also goes from 1.5 microseconds to 2 microseconds to 2.5 microseconds.
4. Despite these differences, they always agree on which events on their own ruler coincide in time and location with which events on the other. If you have a particular clock at a particular location on one ruler showing a particular time, then if you look at the clock right next to it on the other ruler at that moment, you will get the same answer to what that other clock reads and what marking it’s on regardless of which frame you’re using. Here’s one example:
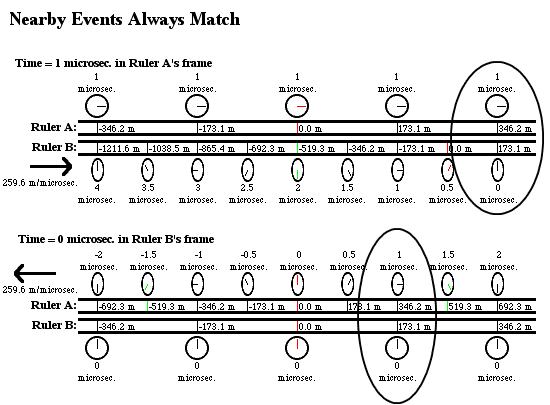
You can look at the diagrams to see other examples, or extrapolate them further in a given direction then I actually drew them, and to later times, to find even more. In every case, two events which coincide in one reference frame also coincide in the other.
A reference frame is really just a coordinate system for marking the location and time of different events. You can think of the physical basis of these coordinates in terms of each observer having a network of rulers and clocks spread throughout space, so if you imagine taking a picture of an event as it happens, its coordinates are defined by the markings on the ruler and the time on the clock right next to the event in the photo. Each observer uses a network of rulers and clocks which are at rest relative to himself. Clocks at different locations must all be synchronized, and in classical physics this would be pretty simple--you could just bring two clocks together to check that they're in sync, then move them to different positions. But time dilation due to movement makes sychronization a little trickier. Einstein's idea was that you could have each observer synchronize their own set of clocks using light signals--pick a point halfway between two clocks, send a flash of light from that point in both directions, and if both clocks read the same time when the light reaches them, they are considered synchronized. But unlike the Galilean frames used in classical physics, this means that the different Lorentzian frames used in relativity will not agree about simultaneity of pairs of events. For example, if an observer on a spaceship sees a flash of light go off in the middle of the ship, then he should synchronize clocks at the front and back of the ship by making sure they both read the same time when the light hits them. But for another observer who sees the ship moving, the back of the ship is moving towards the point where the flash happened and the front is moving away from that point, so his own network of clocks will be synchronized in such a way that the clock next to the event "light hits the back of the ship" will read an earlier time than the clock next to the event "light hits the front of the ship".
Here are some diagrams which may help explain how different reference frames could each see the other's rulers contracted and the other's times dilated without leading to any contradictions. In this example, we have two rulers with clocks mounted on them moving alongside each other, and in order to make the math work out neatly, the relative velocity of the two rulers is (square root of 3)/2 * light speed, or about 259.628 meters per microsecond. This means that each ruler will observe the other one’s clocks tick exactly half as fast as their own, and will see the other ruler's distance-markings to be squashed by a factor of two. Also, I have drawn the markings on the rulers at intervals of 173.085 meters apart—the reason for this is again just to make things work out neatly, it will mean that observers on each ruler will see the other ruler moving at 1.5 markings/microsecond relative to themselves, and that an observer on one ruler will see clocks on the other ruler that are this distance apart (as measured by his own ruler) to be out-of-sync by exactly 1 microsecond, some more nice round numbers.
Given all this, here is how the situation would look at 0 microseconds, 1 microsecond, and 2 microseconds, in the frame of ruler A:
And here’s how the situation would look at 0 microseconds, 1 microsecond, and 2 microseconds, in the frame of ruler B:
Some things to notice in these diagrams:
1. in each ruler's frame, it is at rest while the other ruler is moving sideways at 259.6 meters/microsecond (ruler A sees ruler B moving to the right, while ruler B sees ruler A moving to the left).
2. In each ruler's frame, its own clocks are all synchronized, but the other ruler's clocks are all out-of-sync.
3. In each ruler's frame, each individual clock on the other ruler ticks at half the normal rate. For example, in the diagram of ruler A’s frame, look at the clock with the green hand on the -519.3 meter mark on ruler B--this clock first reads 1.5 microseconds, then 2 microseconds, then 2.5 microseconds. Likewise, in the diagram of ruler B’s frame, look at the clock with the green hand on the 519.3 meter mark on ruler A—this clock also goes from 1.5 microseconds to 2 microseconds to 2.5 microseconds.
4. Despite these differences, they always agree on which events on their own ruler coincide in time and location with which events on the other. If you have a particular clock at a particular location on one ruler showing a particular time, then if you look at the clock right next to it on the other ruler at that moment, you will get the same answer to what that other clock reads and what marking it’s on regardless of which frame you’re using. Here’s one example:
You can look at the diagrams to see other examples, or extrapolate them further in a given direction then I actually drew them, and to later times, to find even more. In every case, two events which coincide in one reference frame also coincide in the other.