lorenz0
- 151
- 28
- Homework Statement
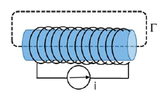
- An iron cylinder with section ##S = 10 cm^2## and length ##d = 20 cm## is uniformly magnetized being placed into a solenoid with ##200## turns around the surface of the cylinder and traversed by a current ##i##. The magnetic field that is measured inside the cylinder is ##H = 10^3 A / m## and ##\oint_{\Gamma} \vec{B}\cdot d\vec{l}= 8\cdot 10^{-4} T m##.
Calculate the current ##i## flowing in the circuit and the magnetization vector ##\vec{M}##.
- Relevant Equations
- ##\oint_{\Gamma}\vec{H}\cdot d\vec{l}=\sum I##, ##\vec{H}=\frac{\vec{B}-\mu_0\vec{M}}{\mu_0}##
From ##\oint_{\Gamma}\vec{H}\cdot d\vec{l}=\sum I## by Ampere's Law which gives ##H \Delta l=\Delta N\cdot i\Leftrightarrow H=n i## where ##n=## number of turns per unit length so ##i=\frac{H}{n}=\frac{10^3 A / m}{\frac{200}{0.2m}}=1 A##.
Since ##\vec{H}=\frac{\vec{B}-\mu_0\vec{M}}{\mu_0}## we also get ##\oint_{\Gamma}\vec{H}\cdot d\vec{l}=\frac{1}{\mu_0}\oint_{\Gamma}(\vec{B}-\mu_0\vec{M})\cdot d\vec{l}\Leftrightarrow \oint_{\Gamma}\vec{M}\cdot d\vec{l}=\frac{1}{\mu_0}\oint_{\Gamma}\vec{B}\cdot d\vec{l}-ni\Leftrightarrow M=\frac{1}{\mu_0}\oint_{\Gamma} \vec{B}\cdot d\vec{l}-\frac{n}{l}i=\frac{1}{4\pi\cdot 10^{-7} H/m}\cdot (8\cdot 10^{-4}Tm)-\frac{200}{0.2m}1 A## ... this last part doesn't really convince me, even dimensionally, even if it looks like the initial idea to use Ampere's Law and then make the substitution ##\vec{H}=\frac{\vec{B}-\mu_0\vec{M}}{\mu_0}## does make sense?
Is there a way to amend my work? I would like to understand how to work with magnetic fields in matter like in this case and I would be grateful for an explanation about how to do that. Thanks
Since ##\vec{H}=\frac{\vec{B}-\mu_0\vec{M}}{\mu_0}## we also get ##\oint_{\Gamma}\vec{H}\cdot d\vec{l}=\frac{1}{\mu_0}\oint_{\Gamma}(\vec{B}-\mu_0\vec{M})\cdot d\vec{l}\Leftrightarrow \oint_{\Gamma}\vec{M}\cdot d\vec{l}=\frac{1}{\mu_0}\oint_{\Gamma}\vec{B}\cdot d\vec{l}-ni\Leftrightarrow M=\frac{1}{\mu_0}\oint_{\Gamma} \vec{B}\cdot d\vec{l}-\frac{n}{l}i=\frac{1}{4\pi\cdot 10^{-7} H/m}\cdot (8\cdot 10^{-4}Tm)-\frac{200}{0.2m}1 A## ... this last part doesn't really convince me, even dimensionally, even if it looks like the initial idea to use Ampere's Law and then make the substitution ##\vec{H}=\frac{\vec{B}-\mu_0\vec{M}}{\mu_0}## does make sense?
Is there a way to amend my work? I would like to understand how to work with magnetic fields in matter like in this case and I would be grateful for an explanation about how to do that. Thanks