An object on an incline of 20° (degrees)

[vizakenjack]

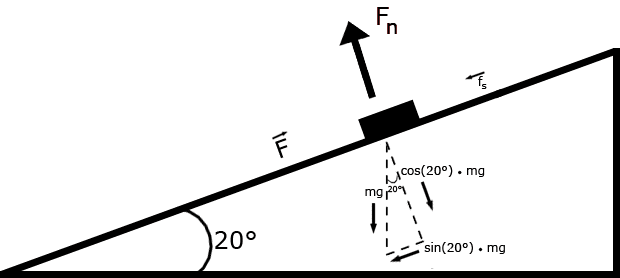
A loaded sled weighing 80N rests on a plane inclined at angle θ= 20° to the horizontal (see pic). Between the sled and the plane, the coefficient of static friction is 0.25, and the coefficient of kinetic friction is 0.15

Taken from http://www.uh.edu/%7Ewkchu/courses/phys1321/chapter6/Home%20Work%206%20Solutions.pdf , problem #16.
a) What is the least magnitude of the force parallel to the plane, that will prevent the sled from slipping down the plane?
b) What is the minimum magnitude F that will start the sled moving up the plane?

Now, I see what the solutions are, but I'm just trying to make sense of them.

So I decided to break up the object's force acting downwards (mg) into x and y components. x = sin(20°) * mg, y =
cos(20°) * mg. In other words, this is how the object's downward force acts in each of those x and y directions.Since the object is on an incline, normal force isn't simply equal to the magnitude of the object's downward force due to gravity in opposite direction (-mg), in this case, normal force - F_n, would only experience an object's partial downward force, which is as you can see from the graph is cos(20°) * mg, which is equivalent to the object's y component of the downward force due to gravity.

So the first question basically asks you how much force is necessary to apply to the object up the incline for it to remain at rest.
Let's see, the normal force (F_n) already takes care of the y component of the object's downward force generated by gravity. So you'd only need to overcome the remaining x component of the object's downward force (sin(20°) * mg), correct? At this point, friction is out of the calculations because the object doesn't need to be moving, but rather remain at rest / stationary on the incline.

But for some reason, they add up the friction force to the Force that needs to be applied, why? It's as if "friction" is helping us when we apply force to the object... which doesn't make sense. Friction does the opposite, when we apply force, our force needs to OVERCOME friction in order to get the object moving up an incline.
Can someone elaborate on this?

 

[Mark44]

So I decided to break up the object's force acting downwards (mg) into x and y components. x = sin(20°) * mg, y =
cos(20°) * mg. In other words, this is how the object's downward force acts in each of those directions x and y directions.

Those aren't x and y components, assuming the base of the triangle in your drawing is lying along the x-axis. The two components would be the tangential component (along the slope) and the normal component (straight into the slope). The weight, mg, acts straight down. That vector can be decomposed into the two components I described.

So the first question basically asks you how much force is necessary to apply to the object up the incline for it to remain at rest.
Let's see, the normal force (Fn) already takes care of the y component of the object's downward force generated by gravity. So you'd only need to overcome the remaining x component of the object's downward force (sin(20°) * mg), correct? At this point, friction is out of the calculations because the object doesn't need to be moving, but rather remain at rest / stationary on the incline.

But for some reason, they add up the friction force to the Force that needs to be applied, why? It's as if "friction" is helping us when we apply force to the object... which doesn't make sense. Friction does the opposite, when we apply force, our force needs to OVERCOME friction in order to get the object moving up an incline.
Can someone elaborate on this?

If there were no friction, to push the block up the plane, you would need to apply a force of magnitude equal to (but oppositely directed) the tangential force acting down the plane. Since there is friction, though, you will need to apply more force. To prevent the sled from slipping down the plane, friction is helping you -- you don't need to apply as much force as the tangential component down the incline.

 

[Chestermiller]

Consider this question: What value would the frictional force need to have to prevent the sled from sliding down the incline? Would this frictional force exceed the coefficient of static friction times the normal force. If not, then the sled will slide down the incline on its own. To keep it from sliding, you would have to provide an additional force up the incline to hold the sled in place.

Chet

 

[vizakenjack]

Those aren't x and y components, assuming the base of the triangle in your drawing is lying along the x-axis. The two components would be the tangential component (along the slope) and the normal component (straight into the slope). The weight, mg, acts straight down. That vector can be decomposed into the two components I described.

But I still need to somehow identify sides of the "decomposed" components of the object's force acting downwards due to gravity. What should I call them, if not x and y?
Tangential component 1 and 2?

If there were no friction, to push the block up the plane, you would need to apply a force of magnitude equal to (but oppositely directed) the tangential force acting down the plane. Since there is friction, though, you will need to apply more force. To prevent the sled from slipping down the plane, friction is helping you -- you don't need to apply as much force as the tangential component down the incline.

Consider this question: What value would the frictional force need to have to prevent the sled from sliding down the incline? Would this frictional force exceed the coefficient of static friction times the normal force. If not, then the sled will slide down the incline on its own. To keep it from sliding, you would have to provide an additional force up the incline to hold the sled in place.
Chet

Exactly what I was thinking.

Component of the object's force acting downwards that isn't taken care of by the F_n (normal force) is still acting on the object (sin(20°) * mg).
But(!) there is friction on the incline, which means that this component sin(20°) * mg needs to overcome friction in order to make the object slide down the incline.
Right?

So, sin(20°) * mg is obviously bigger than the force of friction f_s since the object is going to slide down the incline on its own.
Therefore, we need to apply a force that makes up for the difference between frictional force (f_s) and the component of the object's downward force (sin(20°) * mg) that is acting on the object.

Right?
If it's so, then: sin(20°) * mg (component of the object's downward force) - f_s (frictional force)

f_s = μ_s * F_n
F_n = cos(20°) * mg
m(mass) = 8.16 kg

f_s = 0.25 * cos(20°) * mg = 18.79 Newtons

sin(20°) * mg - 18.79N = 27.35N - 18.79N = 8.56N

Hm... it's pretty much is the same answer that is over http://www.uh.edu/~wkchu/courses/phys1321/chapter6/Home%20Work%206%20Solutions.pdf .But what they basically said is the following: x Newtons is the force you need to apply to the object up the incline, then, x Newtons should make up for the difference between sin(20°) * mg and frictional force.
sin(20°) * mg - f_s) = xN
moving xN to the left side:
sin(20°) * mg - xN - f_s) = 0
multiplying everything by -1
xN -sin(20°) * mg + f_s)
holy sh*t! I've got it!

 

[Chestermiller]

Exactly what I was thinking.

Component of the object's force acting downwards that isn't taken care of by the F_n (normal force) is still acting on the object (sin(20°) * mg).
But(!) there is friction on the incline, which means that this component sin(20°) * mg needs to overcome friction in order to make the object slide down the incline.
Right?

No. The friction force is acting in the opposite direction that the sled wants to slide. So the friction force on the sled is acting up the incline. So the friction force only needs to match the component of the sled weight along the incline.

So, sin(20°) * mg is obviously bigger than the force of friction f_s since the object is going to slide down the incline on its own.
Therefore, we need to apply a force that makes up for the difference between frictional force (f_s) and the component of the object's downward force (sin(20°) * mg) that is acting on the object.

Right?

Yes.

If it's so, then: sin(20°) * mg (component of the object's downward force) - f_s (frictional force)

f_s = μ_s * F_n
F_n = cos(20°) * mg
m(mass) = 8.16 kg

f_s = 0.25 * cos(20°) * mg = 18.79 Newtons

sin(20°) * mg - 18.79N = 27.35N - 18.79N = 8.56N

Hm... it's pretty much is the same answer that is over http://www.uh.edu/~wkchu/courses/phys1321/chapter6/Home%20Work%206%20Solutions.pdf .

So they basically said: x Newtons is the force you need to apply to the object up the incline, then, x Newtons should make up for the difference between sin(20°) * mg and frictional force.
sin(20°) * mg - f_s) = xN
moving xN to the left side:
sin(20°) * mg - xN - f_s) = 0
multiplying everything by -1
xN -sin(20°) * mg + f_s
I've got it!

Nice job.

Chet

 

[Mark44]

Those aren't x and y components, assuming the base of the triangle in your drawing is lying along the x-axis. The two components would be the tangential component (along the slope) and the normal component (straight into the slope). The weight, mg, acts straight down. That vector can be decomposed into the two components I described.

But I still need to somehow identify sides of the "decomposed" components of the object's force acting downwards due to gravity. What should I call them, if not x and y?
Tangential component 1 and 2?

Please reread what I wrote.

 

[vizakenjack]

Please reread what I wrote.

so what I referred to as x was tangential component, and y was the normal component of ... the force exerted by the object's weight downwards due to gravity?

 

[Mark44]

so what I referred to as x was tangential component, and y was the normal component of ... the force exerted by the object's weight downwards due to gravity?

Yes.