- #1
postfan
- 259
- 0
Homework Statement
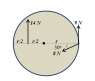
A solid disc of mass m = 5.0 kg and radius r = 0.45 m is spinning clockwise about the axis passing through the center of the disc. At t = 0, three forces are applied to the disc as shown.
Part 1. What is the magnitude of the net torque acting on the disc about its center?
Part 2. Immediately after the three forces are applied, is the magnitude of the angular momentum of the disc increasing, decreasing or staying the same?
Part 3. Assuming that the net torque stays constant, what is the change in the magnitude of the angular momentum of the disc between t = 0 and t = 1.2 s?
Part 4. What is the change in the magnitude of the angular speed between t = 0 and the moment described in Part 3?
Homework Equations
The Attempt at a Solution
For part 1 (taking counterclockwise to be positive) I found the torque by calculating 14*r/2+9*r-sin(30)*r*8=7*r+9r-4r=12r=12*.45=5.4
For part 2, since the disk is rotating clockwise, adding counterclockwise torques will cause it to reduce its angular momentum.
For part 3, I multiplied the time interval by the change in torque: 5.4*1.2=6.48
What am I doing wrong?