Bob4321
- 4
- 0
<< Mentors have notified the OP to show their Attempt at a Solution >>[/color]
1. Homework Statement
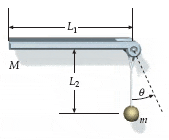
A uniform rod of length L1 = 1.5 m and mass M = 2.8 kg is supported by a hinge at one end and is free to rotate in the vertical plane. The rod is released from rest in the position shown. A particle of mass m is supported by a thin string of length L2 = 1.1 m from the hinge. The particle sticks to the rod on contact. After the collision, θmax= 45°.
a)Find m (in kg)
b) How much energy is dissipated during the collision? (in J)
I found the question with different numbers but when I plug in mine. It's still wrong.
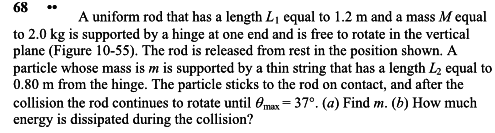

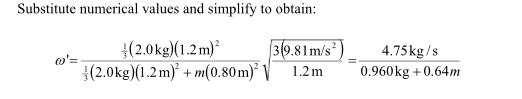

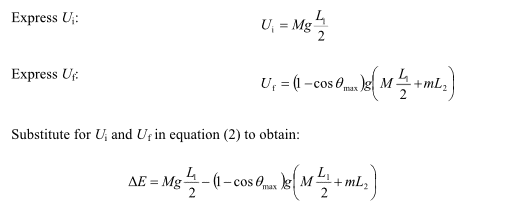
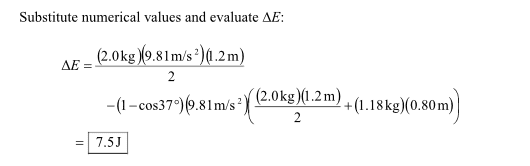
1. Homework Statement
A uniform rod of length L1 = 1.5 m and mass M = 2.8 kg is supported by a hinge at one end and is free to rotate in the vertical plane. The rod is released from rest in the position shown. A particle of mass m is supported by a thin string of length L2 = 1.1 m from the hinge. The particle sticks to the rod on contact. After the collision, θmax= 45°.
a)Find m (in kg)
b) How much energy is dissipated during the collision? (in J)
Homework Equations
I found the question with different numbers but when I plug in mine. It's still wrong.
The Attempt at a Solution
Last edited by a moderator: