Angular Momentum: Uniform Cylinder Drum Rotation

[devious_]

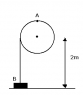
A uniform solid cylindrical drum of mass 1.5kg and radius 0.5m is free to rotate about a fixed, smooth, horizontal axis which coincides with the axis of the cylinder. The axis is at a height of 2m above a horizontal table, and a light string of AB of length 4m has one end attached to the heighest point of the cylinder. A block of mass 0.3kg is attached to end B of the string and rests on the table. The drum begins to rotate at a constant angular speed of 4 rad s^-1 in a clockwise direction. Calculate the angular speed of the drum immediately after the block is jerked into motion.

I have no idea how to approach this question! The answer is supposed to be 2.86 rad s^-1.

Any help is greatly appreciated.

 

[whozum]

I'm looking at this and the only thing i can think of is to find the angular acceleration of the drum due to the block pulling it down.

 

[devious_]

I think the way I'm supposed to approach this question is by equating the sums of initial and final angular momentum for both the drum and the block. I can do the drum just fine, but all my attemps of finding the angular momentum of the block didn't produce the required answer.

Here's what I get for the drum:
initial angular momentum = moment of inertia * angular speed = 3/16 * 4 = 0.75 Nms
final angular momentum = 3/16 w, where w is the new angular speed

 

[whozum]

Ohhh right. Ofcourse.

The final moment of inertia has changed, because its now pulling the block. You can simplify the block as a point mass at point A, and find the new MOI.

 

[devious_]

I tried that:
final angular momentum = [3/16 + 0.3*(2^2 + 0.5^2)] w = 1.4625w
conservation of angular momentum => w = 0.75/1.4625 = 20/39

Which isn't the right answer. Am I doing something wrong?

 

[whozum]

final angular momentum = [3/16 + 0.3*(2^2 + 0.5^2)] w = 1.4625w

Your radius isn't right. How far is the point A from the axis of rotation?

 

[devious_]

If I take it to be at point A then I get the right answer! But.. Why should it be at point A?

 

[devious_]

I thought about it a bit and this is what I concluded:
Initial jerk turns the drum 4 rad, and so the block is pulled up 4*0.5 m, because A turns an arc length r \theta. So the block adheres to the circumference of the circle and can be considered as a point mass 0.5m away from the axis of rotation.

Is this correct?

 

[whozum]

Exactly, the block is 'pulling' or resisting motion AT the radius 0.5m, thus you can treat it as a particle in motion at the edge of the drum. Good thinking.

 

[devious_]

Thanks for the help -- and good night!