Elkay
- 20
- 0
Due to a jaw injury, a patient must wear a strap (see the figure) that produces a net upward force of 5.00 N on his chin. The tension is the same throughout the strap. To what tension must the strap be adjusted to provide the necessary upward force? Here's the picture:
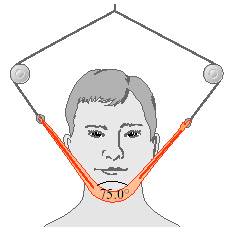
I think the tension for both sides of the strap will be equal, and the sum of all forces should equal zero. I'm also thinking that the sum of all forces should be zero if this is at equilibrium.
This is what I've done so far (hopefully my handwriting isn't too bad):
http://home.earthlink.net/~copper017/Random/freebody.jpg
http://home.earthlink.net/~copper017/Random/equations.jpg
I'm under the impression that this problem should be simple, but I've been looking at it and trying to do different things to it yesterday.
I think the tension for both sides of the strap will be equal, and the sum of all forces should equal zero. I'm also thinking that the sum of all forces should be zero if this is at equilibrium.
This is what I've done so far (hopefully my handwriting isn't too bad):
http://home.earthlink.net/~copper017/Random/freebody.jpg
http://home.earthlink.net/~copper017/Random/equations.jpg
I'm under the impression that this problem should be simple, but I've been looking at it and trying to do different things to it yesterday.
Last edited by a moderator: