gomerpyle
- 40
- 0
Homework Statement
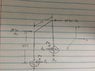
A force couple acts on the frame, which is fixed at the base. Find the moment(s) and reaction(s) at the fixed locations.
Homework Equations
ΣMa = 0
ΣMb = 0
ΣFy = 0
ΣFx = 0
The Attempt at a Solution
Since it would be statically indeterminate, assumptions would be that the reactions are equivalent to the acting forces (1430 lbs), and points of inflection exist halfway along the 25.5" length of the legs? This results in a theoretical "pinned" connection at the center thus the FBD for one leg cut in half:
ΣMa = -(12.75)*1430 + Ma = 0
Ma = 18232 in-lbs
Obviously both moments have to be equal, so Mb = 18232 in-lbs.
Am I on the right track? Wouldn't there be a Torsional reaction as well? I'm just a little lost because all the examples of frames I can find don't have forces acting perpendicular to the plane of the members (acting "into the page").