santeri
- 3
- 0
Hi all!
This isn't actually a homework question, but thought this subforum is the place for this anyway. It's been some ten years since I last touched the topic of mechanics and I guess this is a real simple question, but what can you do when I don't get it! Any help is appreciated!
How do I calculate the forces acting on contact points in situation like the picture?
There is the force from gravity on the object, and another force at some point pushing the object down. Torque in the pic is from the force pushing down on right.
Calculating torque from the force and lever arm is simple yes, but getting that back to forces on the contact points is what baffles me.
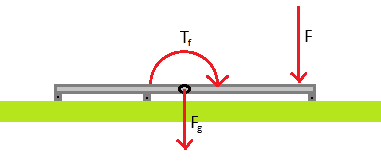
This isn't actually a homework question, but thought this subforum is the place for this anyway. It's been some ten years since I last touched the topic of mechanics and I guess this is a real simple question, but what can you do when I don't get it! Any help is appreciated!
How do I calculate the forces acting on contact points in situation like the picture?
There is the force from gravity on the object, and another force at some point pushing the object down. Torque in the pic is from the force pushing down on right.
Calculating torque from the force and lever arm is simple yes, but getting that back to forces on the contact points is what baffles me.