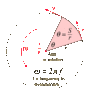Are angular & vertical velocity the same if the objects are connected

AI Thread Summary
In a system where a flywheel is connected to a rod with a mass hanging from it, the angular velocity of the flywheel and the vertical velocity of the hanging mass are related but not the same. As the flywheel rotates, it causes the rod to rotate, which in turn affects the vertical motion of the mass. The vertical velocity of the mass can be derived from the angular velocity of the flywheel through the radius of the rod. The relationship between angular velocity and linear velocity is defined by the equation v = rω, where v is linear velocity, r is the radius, and ω is angular velocity. Understanding this relationship is crucial for analyzing the dynamics of the system.
Isolde Wilde
Messages
6
Reaction score
0
think of a engine. it has a flywheel and a rod connected to it. a string had been totally wrapped around the rod and a mass is hanged from the very end of the rod. the system is in equilibrium. but as the engine starts to rotate, the rod with rotate as well and cause the hanged object to go down while the string comes lose as the rod rotates. is the vertical velocity of the mass hanged equal to the angular velocity of the flywheel?
 
Physics news on Phys.org
What is the relationship between angular and linear velocity? You are leaving off an important term so far...

http://hyperphysics.phy-astr.gsu.edu/hbase/imgmec/avel.gif

avel.gif
 

Attachments

  • avel.gif
    avel.gif
    11.1 KB · Views: 411

Thread '1:1 versus 2:1 Mechanical Advantage debate'

The rope is tied into the person (the load of 200 pounds) and the rope goes up from the person to a fixed pulley and back down to his hands. He hauls the rope to suspend himself in the air. What is the mechanical advantage of the system? The person will indeed only have to lift half of his body weight (roughly 100 pounds) because he now lessened the load by that same amount. This APPEARS to be a 2:1 because he can hold himself with half the force, but my question is: is that mechanical...
View full post »

Thread 'Newton's first law?'

Some physics textbook writer told me that Newton's first law applies only on bodies that feel no interactions at all. He said that if a body is on rest or moves in constant velocity, there is no external force acting on it. But I have heard another form of the law that says the net force acting on a body must be zero. This means there is interactions involved after all. So which one is correct?
View full post »
Thread 'Beam on an inclined plane'

Thread 'Beam on an inclined plane'

Hello! I have a question regarding a beam on an inclined plane. I was considering a beam resting on two supports attached to an inclined plane. I was almost sure that the lower support must be more loaded. My imagination about this problem is shown in the picture below. Here is how I wrote the condition of equilibrium forces: $$ \begin{cases} F_{g\parallel}=F_{t1}+F_{t2}, \\ F_{g\perp}=F_{r1}+F_{r2} \end{cases}. $$ On the other hand...
View full post »

Similar threads

I Angular velocity of a rod and what formula to use while solving.
Replies
15
Views
2K
I Conservation of angular momentum during collisions
Replies
3
Views
3K
B What is physical significance of the direction of angular velocity?
Replies
2
Views
1K
I Equation of motion for a simple mechanical system
Replies
2
Views
2K
Conceptual questions about Angular Momentum Conservation and torque
Replies
2
Views
2K
I Mechanics of an inertial balance
Replies
6
Views
1K
B The physics of flywheel launchers (like tennis ball shooters)
2
Replies
60
Views
4K
Why Doesn't the Ball Rotate When Hit by a Pivoting Rod?
Replies
30
Views
3K
Relative angular velocity in a rotating rod
Replies
4
Views
3K
Torque and Moment of Inertia of a Lever Arm
Replies
2
Views
3K

Hot Threads

Recent Insights

Back
Top