Area of overlapping polar coordinates

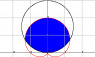
[ex81]

Homework Statement

find the over lapping area of the following equations

r=3sin(x)
r=1+sin(x)

Homework Equations

area =1/2 ∫ f(x)^2 dx

The Attempt at a Solution

first off I started by finding the intersecting angle by:
3sin(x)=1+sin(x)
2sin(x)=1
sin(x)=1/2
x=pi/6

and the peak is at pi/2

so I started with a = 2×1/2 ∫ (1+sin(x))^2 dx from pi/6 to pi/2

so (3/2)x-2cos(x) -1/4 sin(x) from pi/6 to pi/2
comes out to 2pi/4 + (7√3)/8

then I have the other segment

a= 2×1/2 ∫ (3sin(x))^2 dx from 0 to pi/6
(9/2)x-(9/2)sin(2x)

for which I get 3pi/4 - (9√3)/8

which totals up to 7pi/4 -(2√3)/8

and according to my professor's key the answer is pi

needless to say I am lost.

 

[DryRun]

You should always plot the graph to easily understand and deduce the limits. I have attached the graph and the overlapped area is shaded in blue.

You could use the formula for area of sector of a circle, but the problem will become longer than needed.

Calculating the half area on the right of the line ∏/2 using polar coordinates:
$$Half\; area\;=\int^{x=\pi /2}_{x=0} \int^{r=1+\sin x}_{r=0} rdrdx-<br /> \int^{x=\pi /6}_{x=0} \int^{r=1+\sin x}_{r=3\sin x} rdrdx$$ Then, multiply by 2.

Now, using the method involving the formula for area of sector of a circle:

First, find the area from x = 0 to x=∏/2 inside the cardioid.
$$\frac{1}{2}\int^{x=\pi /2}_{x=0} (1+\sin x)^2dx$$
Then, you need to find the small area wedged between both graphs, in the interval x=0 and x=∏/6
$$\frac{1}{2}\int^{x=\pi /6}_{x=0} (1+\sin x)^2dx-\frac{1}{2}\int^{x=\pi /6}_{x=0} (3\sin x)^2dx$$
Finally, subtract area of wedge from cardioid, to get the half area, then multiply by 2 to get the total overlapping area.

There is still another way (a shorter version) of doing this problem using the area of sector formula:

First, find the area of sector inside cardioid from x=∏/6 to x=∏/2:
$$\frac{1}{2}\int^{x=\pi /2}_{x=\pi / 6} (1+\sin x)^2dx$$
Then, find the area inside circle from x=0 to x=∏/6:
$$\frac{1}{2}\int^{x=\pi /6}_{x=0} (3sin x)^2dx$$
Add them up and multiply by 2.
You could also write its equivalent in terms of polar coordinates.

 

[ex81]

Thanks but that is actually doing. I think I am messing up the integration somewhere. It is just hard to type this all out on a tablet.

 

[DryRun]

so I started with a = 2×1/2 ∫ (1+sin(x))^2 dx from pi/6 to pi/2

so (3/2)x-2cos(x) -1/4 sin(x) from pi/6 to pi/2
comes out to 2pi/4 + (7√3)/8

$$2\times \frac{1}{2}\int^{x=\pi /2}_{\pi /6} (1+\sin x)^2 \,.dx=\int^{x=\pi /2}_{\pi /6} (1+\sin x)^2 \,.dx=\int^{x=\pi /2}_{\pi /6} (1+2\sin x+\sin^2x) \,.dx=\frac{\pi}{2}+\frac{9\sqrt 3}{8}$$

then I have the other segment

a= 2×1/2 ∫ (3sin(x))^2 dx from 0 to pi/6
(9/2)x-(9/2)sin(2x)

for which I get 3pi/4 - (9√3)/8

$$\int^{x=\pi /6}_{x=0} (3\sin x)^2\,.dx=\int^{x=\pi /6}_{x=0} 9\sin^2x\,.dx=\frac{3\pi}{4}-\frac{9\sqrt 3}{8}$$
Adding them up, the total area is: $\frac{5\pi}{4}$

 

[ex81]

Thanks, so I did make at least one mistake :-D