Freeq
- 7
- 0
Homework Statement
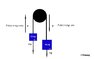
Smaller mass on an Atwood machine is 5.2 kg (m1). If the mass accelerates at 4.6 m/s2what is the mass of the object? What is the tension of the rope?
Homework Equations
a = g(m2-m1)/(m2+m1)
The Attempt at a Solution
I can't approach this questions, because we always worked with two masses and had to find acceleration and tension of the string, but we have never worked without the second mass.