- #1
cala
- 194
- 0
Hi. I saw this video on google:
http://video.google.com/videoplay?docid=6377655322209610872
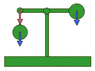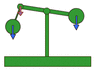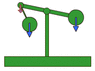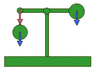
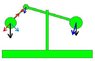
It's mainly a pendulum attached to a balance arm.
It's stated that the energy needed to keep the pendulum going is far less than the energy we can extract from the balance movement.
I also post some pictures to try to show how it 's supposed to work.
This is how i suppose it works:
The force of gravity on the pendulum de-composes into two components as it oscillates: one is tangential acceleration, that keeps the oscillation going and the other one is a perpendicular force to the pendulum "track".
When the pendulum is in vertical position, tangential force is 0, and perpendicular force is at maximum value. When the pendulum is at the 2 top points of its path, the tangential force is at maximum value, and the perpendicular one is at the minimum.
The perpendicular force doesn't affects the pendulum's oscillations. Only the tangential component maintains the pendulum oscillating. Usually, the perpendicular force is compensated with an opposite force on the "strongpoint" of the pendulum... But what happens if we put the "strongpoint" of the pendulum pending from an arm of a balance? It's exactly the same as if we put a "variable weight" on this side of the balance, so the other side of the balance (if it has a fixed weight) will move up and down, just as if we put more or less weight on the side of the pendulum.
So the question is: Why it's needed more energy to keep the pendulum oscillating than the work we can extract from the movement of the balance by the "variable weight" that is on the pendulum's side of the balance?
The variation of the perpendicular component of the pendulum's weight is just a consequence of the pendulum oscillation, and usually, it's not used to do anything. But this perpendicular component can take values from 100% to 10% of the total weight of the pendulum while the pendulum is oscillating. So why the input work (for maintain the oscillation) should be equal or higher than the work we can extract from the balance movement by using the "variable weight" of the perpendicular force?
Do you know an expresion that relates the loses on the pendulum's oscillation and the work on the balance?
Can you explain why the work the perpendicular component can do have to be less than the loses we have to restore on the pendulum's oscillation?
Thank you.
http://video.google.com/videoplay?docid=6377655322209610872
It's mainly a pendulum attached to a balance arm.
It's stated that the energy needed to keep the pendulum going is far less than the energy we can extract from the balance movement.
I also post some pictures to try to show how it 's supposed to work.
This is how i suppose it works:
The force of gravity on the pendulum de-composes into two components as it oscillates: one is tangential acceleration, that keeps the oscillation going and the other one is a perpendicular force to the pendulum "track".
When the pendulum is in vertical position, tangential force is 0, and perpendicular force is at maximum value. When the pendulum is at the 2 top points of its path, the tangential force is at maximum value, and the perpendicular one is at the minimum.
The perpendicular force doesn't affects the pendulum's oscillations. Only the tangential component maintains the pendulum oscillating. Usually, the perpendicular force is compensated with an opposite force on the "strongpoint" of the pendulum... But what happens if we put the "strongpoint" of the pendulum pending from an arm of a balance? It's exactly the same as if we put a "variable weight" on this side of the balance, so the other side of the balance (if it has a fixed weight) will move up and down, just as if we put more or less weight on the side of the pendulum.
So the question is: Why it's needed more energy to keep the pendulum oscillating than the work we can extract from the movement of the balance by the "variable weight" that is on the pendulum's side of the balance?
The variation of the perpendicular component of the pendulum's weight is just a consequence of the pendulum oscillation, and usually, it's not used to do anything. But this perpendicular component can take values from 100% to 10% of the total weight of the pendulum while the pendulum is oscillating. So why the input work (for maintain the oscillation) should be equal or higher than the work we can extract from the balance movement by using the "variable weight" of the perpendicular force?
Do you know an expresion that relates the loses on the pendulum's oscillation and the work on the balance?
Can you explain why the work the perpendicular component can do have to be less than the loses we have to restore on the pendulum's oscillation?
Thank you.
Attachments
Last edited by a moderator: