peripatein
- 868
- 0
Hello,
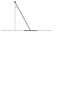
A uniform bar of mass m is hinged to the ceiling and rests on a smooth floor at an angle α with respect to the vertical axis (please see attachment). A thin sheet of paper, with coefficient of friction μ, is inserted between the floor and the bar.
What is the minimum force necessary to pull the paper to the right?
What is the minimum force necessary to pull the paper to the left?
Obviously I must figure out which forces are in action before analysing the torques.
The forces acting on the bar are:
N1, in the positive y direction (i.e. up), at the point where the bar is in contact with the floor; fs, acting on the bar at that contact point with the floor, in the negative x direction (i.e. to the left); W, from the center of mass of the rod, in the negative y direction. Is that all? Are there any forces acting on the bar at the point where it is hinged to the ceiling?
Homework Statement
A uniform bar of mass m is hinged to the ceiling and rests on a smooth floor at an angle α with respect to the vertical axis (please see attachment). A thin sheet of paper, with coefficient of friction μ, is inserted between the floor and the bar.
What is the minimum force necessary to pull the paper to the right?
What is the minimum force necessary to pull the paper to the left?
Homework Equations
The Attempt at a Solution
Obviously I must figure out which forces are in action before analysing the torques.
The forces acting on the bar are:
N1, in the positive y direction (i.e. up), at the point where the bar is in contact with the floor; fs, acting on the bar at that contact point with the floor, in the negative x direction (i.e. to the left); W, from the center of mass of the rod, in the negative y direction. Is that all? Are there any forces acting on the bar at the point where it is hinged to the ceiling?