benjaminwhite
- 7
- 0
Homework Statement
Consider the downhill skier shown at the right (just a picture of a skier, no info given in picture). The skier has a mass of 77kg and is traveling at 45mph.
Neglecting friction and drag, calculate the skier's acceleration. Explain and justify any measurements, assumptions, approximations you make.
Homework Equations
F=ma
The Attempt at a Solution
I've tried a number of different things.
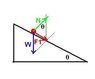
I started with a free body diagram, showing F1 moving down and to the right, w pointing straight down, and N pointing perpendicular to F1.
I then put an x y axes with the x-axis running along F1 and the y-axis along N, with W now pointing down and to the right.
I broke W into components, which didn't seem to help as I don't have enough info.
y
|N
|
|_______ x
|\ F1
| \ W
Wy | \
|_(\ <--- called this angle theta
Wx
To do that I did Cos(theta)=Wx/W
so W(cos theta) = Wx
and similary sin(theta)=Wy/W
so W(sin theta)=Wy
x | y
+F1 | +N
+W(costheta)| -w(sintheta)
I can find that N = W(sin theta) by doing
Fynet = may
ay = 0
so Fynet = 0
N - W(sintheta) = 0
N = W(sintheta)
To solve for Fxnet all I can get is
Fxnet = may
F1+W(cos theta)=max
so (F1+W(costheta))=ax
As you can see I'm pretty confused, I don't feel like that's the right answer and that I'm missing something.