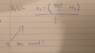CoolDude420
- 199
- 9
Homework Statement
Hi,
So I'm just curious whether or not the following statement is correct for the circuit shown. It's part of a bigger problem involving OP-AMPS, the part of the circuit shown is the upper loop connecting from the inverting to the output.
I was just having some doubts in my mind and wanted to confirm whether or not the equation i have written is correct.
Homework Equations
Ohms Law. V = IR.