OneTimePad
- 2
- 0
Hello all,
I just came across a problem that I had previously solved. A relatively simple one. What I do not understand though is why I can use the equation that I have used so many times in this particular situation. Here it is:
A baseball pitcher throws a baseball with a speed of 41 m/s. Estimate the average acceleration of the ball during the throwing motion. In throwing the baseball, the pitcher accelerates the ball through a displacement of about 3.5 m, from behind the body to the point where it is released.
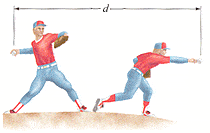
V0 = 0 m/s
Vf = 41 m/s
d (Xf - Xi) = 3.5m
Equation for motion at constant acceleration:
( Vf2 - V02 ) / 2d = a
412 / (2*3.5) = 240.14 m/s2
My question is: Why can I use this equation in the first place? Aren't these equations only valid if the acceleration is constant? Where in the problem does it suggest that the 'average acceleration of the ball during the throwing motion' is indeed constant?
Any insights would be greatly appreciated.
Thanks in advance.
I just came across a problem that I had previously solved. A relatively simple one. What I do not understand though is why I can use the equation that I have used so many times in this particular situation. Here it is:
Homework Statement
A baseball pitcher throws a baseball with a speed of 41 m/s. Estimate the average acceleration of the ball during the throwing motion. In throwing the baseball, the pitcher accelerates the ball through a displacement of about 3.5 m, from behind the body to the point where it is released.
V0 = 0 m/s
Vf = 41 m/s
d (Xf - Xi) = 3.5m
Homework Equations
Equation for motion at constant acceleration:
( Vf2 - V02 ) / 2d = a
The Attempt at a Solution
412 / (2*3.5) = 240.14 m/s2
My question is: Why can I use this equation in the first place? Aren't these equations only valid if the acceleration is constant? Where in the problem does it suggest that the 'average acceleration of the ball during the throwing motion' is indeed constant?
Any insights would be greatly appreciated.
Thanks in advance.