sirclash
- 7
- 0
1. Where did i go wrong, please explain.
Homework Statement
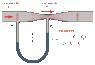
The Horizontal Venturi pipe has a cross sectional area of 50cm^2 at the wider portions(A_1) and 25cm^2 at the constriction(A_2). Air density of 1.29 kg/(m^3) is flowing in the pipe.
Theres a attachment of a picture to reference.
A)Write down Bernoulli's equation for the streamline of the wider part to the streamline of the constricted part.
B)Derive an expression for the speed of the air, V_2 (Constricted), in terms of the cross sectional area A_1 and A_2, The pressure difference (P_1 - P_2), and the density of air (roh).
C) The difference in height, h, of the columns in the U-shaped tube is 15 cm. Find the pressure difference given the density of mercury is 13600 kg/(m^3)
D) Calculate V_2
P_1 + (roh*V_1^2)/2 + roh*g*y_1= P_2 + (roh*V_2^2)/2 + roh*g*y_2
A) P_1 + (roh*V_1^2)/2 = P_2 + (roh*V_2^2)/2
B) I rearranged the the answer and used V_1=(A_2*V_2)/(A_1) to get,
V_2= (2(P_1 - P_2))/(roh(1-(A_2)/(A_1))^2) is this right??
C) P_1 - P_2 = (roh of mercury)*g*h i get P_1 - P_2 = 1999.2 pascals?
D) I got 1033.17 m/s and that can be right unless i just converted wrong.
Homework Statement
The Horizontal Venturi pipe has a cross sectional area of 50cm^2 at the wider portions(A_1) and 25cm^2 at the constriction(A_2). Air density of 1.29 kg/(m^3) is flowing in the pipe.
Theres a attachment of a picture to reference.
A)Write down Bernoulli's equation for the streamline of the wider part to the streamline of the constricted part.
B)Derive an expression for the speed of the air, V_2 (Constricted), in terms of the cross sectional area A_1 and A_2, The pressure difference (P_1 - P_2), and the density of air (roh).
C) The difference in height, h, of the columns in the U-shaped tube is 15 cm. Find the pressure difference given the density of mercury is 13600 kg/(m^3)
D) Calculate V_2
Homework Equations
P_1 + (roh*V_1^2)/2 + roh*g*y_1= P_2 + (roh*V_2^2)/2 + roh*g*y_2
The Attempt at a Solution
A) P_1 + (roh*V_1^2)/2 = P_2 + (roh*V_2^2)/2
B) I rearranged the the answer and used V_1=(A_2*V_2)/(A_1) to get,
V_2= (2(P_1 - P_2))/(roh(1-(A_2)/(A_1))^2) is this right??
C) P_1 - P_2 = (roh of mercury)*g*h i get P_1 - P_2 = 1999.2 pascals?
D) I got 1033.17 m/s and that can be right unless i just converted wrong.