Aleolomorfo
- 70
- 4
Homework Statement
##\alpha##-Centuary is in a binary visual system with another star. Their separation, from their CM, is 8.0'' and 9.7''. The distance from the Earth is 1.31pc. Their revolution period around the CM is 80.1 years. I have to find masses and luminosities for each star.
Homework Equations
Third Newton's law: ##\omega^2 = \frac{G(M_1+M_2)}{a^3}##
The Attempt at a Solution
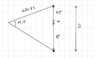
With the help of this picture I can calculate ##a=1.7''\times1.31pc##. Then I can solve this system of equations:
$$\omega^2 = \frac{G(M_1+M_2)}{a^3}$$
$$\omega = \frac{2\pi}{T}$$
In this way I find only ##M_1+M_2##. I need another equation but I do not find it.
For the luminosity I can use the scaling relation that ##L\propto M^4##. However, firstly I need to find ##M_1## and ##M_2## separately.