peasngravy
- 72
- 6
- Homework Statement
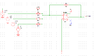
- FIGURE 2(a) shows a ‘black box’ that is to partially synthesise a ‘sawtooth’ waveform of FIGURE 2(b) by using the Fourier series
algorithm:
- Relevant Equations
- v(t) = 2/pi(sin.omega.t)
Hi
I received some great help yesterday and i was hoping someone would be able to help me out again today
Note: the given equation is very long and would look very messy without being typed in the correct format so I didn't enter the entire thing in the relevant equations box; instead it is included in the screenshot below

I am not sure at all what is being asked of me here. There are no Fourier algorithms in any of my notes so I am struggling with what I can do with this.
What I know so far is that the amplitude is 5 volts, and the frequency is 1000hz (1 cycle per ms on the graph).
Could someone please explain how I should use the Fourier algorithm to find my answer?
Thanks
I received some great help yesterday and i was hoping someone would be able to help me out again today
Note: the given equation is very long and would look very messy without being typed in the correct format so I didn't enter the entire thing in the relevant equations box; instead it is included in the screenshot below

I am not sure at all what is being asked of me here. There are no Fourier algorithms in any of my notes so I am struggling with what I can do with this.
What I know so far is that the amplitude is 5 volts, and the frequency is 1000hz (1 cycle per ms on the graph).
Could someone please explain how I should use the Fourier algorithm to find my answer?
Thanks