BWE38
- 10
- 0
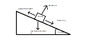
A 40.8 kg box is being pulled up a 13.5 deg slope by a force of 294 N which is parallel to the slope. The coeffcient of kinetic friction between the box and the slope is 0.21. what is the acceleration of the box?
-----------------------------------------------------
Equations: F=MA, Fk=μk(MA)
-----------------------------------------------------
Attemped at the solution
deg= 13.5 M= 40.8 kg F=294 μκ= 0.21
force x-direct---------------------------------------force y-direct
294(cos13.5)(0.21)=(40.8 kg)A------------------294(sin13.5)(.21)=(40.8)A
60.03=40.8A---------------------------------------14.41=40.8A
A=1.47 m/s^2-------------------------------------A= 0.35 m/s^2
acceleration= √(1.47^2+0.35^2)
acceleration= 1.51 m/s^2
---------------------------------------------------------
The answer is 2.91 m/s^2, which I don't understand.
-----------------------------------------------------
Equations: F=MA, Fk=μk(MA)
-----------------------------------------------------
Attemped at the solution
deg= 13.5 M= 40.8 kg F=294 μκ= 0.21
force x-direct---------------------------------------force y-direct
294(cos13.5)(0.21)=(40.8 kg)A------------------294(sin13.5)(.21)=(40.8)A
60.03=40.8A---------------------------------------14.41=40.8A
A=1.47 m/s^2-------------------------------------A= 0.35 m/s^2
acceleration= √(1.47^2+0.35^2)
acceleration= 1.51 m/s^2
---------------------------------------------------------
The answer is 2.91 m/s^2, which I don't understand.
Last edited: