- #1
lindzzz
- 4
- 0
Homework Statement
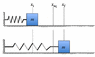
A block with mass m = 3.57 kg is attached to a spring with spring constant k = 165.7 N/m and negligible mass. The coefficient of kinetic friction between the block and the table is µk = 0.239. The box is displaced from its equilibrium position to the left by 0.216 m. If the block is released from rest, calculate the block's displacement when it first comes to rest again.
(Picture attached)
Homework Equations
Us = 1/2kΔL²
Wfriction = μmgdcosθ
The Attempt at a Solution
This is what I tried:
Us = Wfriction
1/2(k)(xf)² - 1/2(k)(xi)² = μmgdcosθ
I then said xf = d - xi and subbed in this for xf
1/2(165.7)(d-0.216)² - 1/2(165.7)(0.216)² = 0.239(3.57)(9.8)d(cos180°)
solving for d I get d = 0.33 m but this is incorrect
I'm not sure what I'm doing wrong, suggestions?