Bullet stuck into a ball and rotates it

[Karol]

Homework Statement

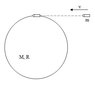
A ball of mass M and radius R can rotate round an axis through it's center. a bullet of mass m travels with speed v, hits the ball near the surface and gets stuck in it.
What's their angular velocity after the collision.

Homework Equations

Moment of inertia of a ball round it's axis: $I=\frac{2}{5}MR^2$
Conservation of angular momentum: $mvR+MVR=0$

The Attempt at a Solution

Conservation of angular momentum:
$$mvR=(M+m)\omega R^2\Rightarrow \omega=\frac{mv}{(m+M)R}$$

 

[stockzahn]

Moment of inertia of a ball round it's axis: I=25MR2

Why didn't you use the ball's moment of inertia?

 

[Karol]

$$mvR=\left( \frac{2}{5}MR^2+mR^2 \right)\omega\Rightarrow \omega=\frac{mv}{R\left( \frac{2}{5}M+m \right)}$$

 

[stockzahn]

To understand it correctly: Does the statement imply that the ball is turning around an axis or is it lying on the ground and rolls away after getting hit by the bullet?

 

[stockzahn]

Sorry, ignore this post (wrong thread)

 

[haruspex]

A ball of mass M and radius R can rotate round an axis through it's center. a bullet of mass m travels with speed v, hits the ball near the surface

I'm struggling to picture how it could have hit it anywhere except near the surface.
(It's ok, I understand what they were trying to say.)