gummybeargirl
- 22
- 0
Homework Statement
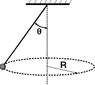
A mass of 3.50 kg is suspended from a 1.59 m long string. It revolves in a horizontal circle as shown in the figure.
The tangential speed of the mass is 2.99 m/s. Calculate the angle between the string and the vertical.
Homework Equations
a_c = v^2/r
F = m*a_c
tanθ=sinθ/cosθ
sin^2θ=1-cos^2θ
The Attempt at a Solution
Vertical: T*cos(θ)-m*g=0 → T=(m*g)/cos(θ)
Horizontal: T*sin(θ) = m*a_c
Combined the two: ((m*g)/cos(θ))sin(θ)=m*a_c → m*g*tan(θ)=m*a_c → g*tan(θ)=a_c
we know that a_c=v^2/r, plug that into get g*tan(θ)=v^2/r
r=L*sin(θ) → g*tan(θ)=v^2/(L*sin(θ))
I cannot get past this point and the notes on the problem say that a quadratic equation needs to be solved at some point.